Selection Sort - Ordenação por seleção
Pra começar, podemos tentar entender quando surge a necessidade de aplicar um algoritmo de ordenação. Por exemplo, você já tentou organizar pessoas de uma lista, em ordem alfabética? Sim, este é um bom exemplo de necessidade de ordenação.
Neste artigo, será enfatizada a ordenação feita através de uma linguagem de programação com a implementação de um algoritmo de ordenação conhecido como selection sort.
O algoritmo selectionsort
O selectionsort é um dos algoritmos de ordenação mais simples de implementar. Vamos a um exemplo!
Suponha o seguinte arranjo de números:
[4, 6, 2, 1, 7, 2]
Através de uma linguagem de programação, se pode armazenar esses números em posições vizinhas da memória. Logo, cada posição da memória com capacidade de armazenar um numero (tipo inteiro), corresponde a parte de uma estrutura de acesso sequencial: Um array unidimensional.
A imagem abaixo ilustra a ordenação do array tomado como exemplo:
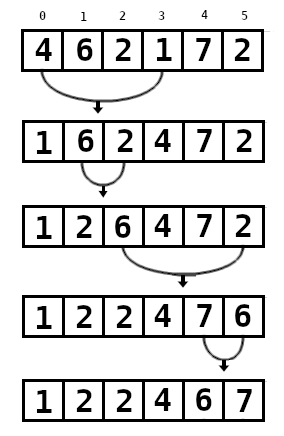
A lógica é muito simples:
- Seleciona-se o menor número e o coloca na primeira posição
- Seleciona-se o segundo menor número e o coloca na segunda posição
- Repetir até chegar a última posição
Pseudocódigo
selectionsort( A, n )for i=0 to n-1 dok = ifor j=i+1 to n-1 doif A[j] < a[k] thenk = iif ( k <> i ) thenaux = A[k]A[k] = A[i]A[i] = aux
Agora vamos a explicação!
Na primeira linha está a definição da função que ordena conforme o algoritmo. A função recebe dois parâmetros: O arranjo A (array unidimensional de inteiros) e o numero inteiro 'n' que corresponde ao tamanho do array.
Na segunda linha está o for principal, cuja variável 'i' varia de 0 até n-1, para que todos os valores do vetor A sejam percorridos. A cada iteração, o menor valor encontrado em posições a partir de 'i', se o valor armazenado em 'i' não já for o menor, é trocado com o valor armazenado em 'i'.
Na terceira linha, o valor de i é armazenado em k e, logo após, na linha seguinte, a variável 'j' do for, varia de 'i+1', até 'n-1'. Isto é, percorre o vetor em todas as posições à frente de 'i'. A cada iteração desse for, o valor armazenado no 'j' da vez é comparado com o menor valor encontrado em elementos com índice igual ou maior que 'i'. O índice desse menor valor é o valor da variável 'k' após a execução dessa parte do algoritmo.
Ao final da execução do for da linha 4, a variável 'k' tem armazenado o índice do menor elemento entre os elementos de índice igual ou maior que 'i'.
Após encontrado o valor de 'k', basta, conforme na linha 7, se o índice do menor valor encontrado a partir de 'i' for diferente de 'i', entao, inverter os valores armazenados em 'i' e em 'k'.
A inversão de valores armazenados em variáveis (ou posições de um vetor) é muito simples. É análoga a trocar o conteúdo de dois copos: O primeiro com leite e o segundo com água. Isto é, o primeiro deve passar a conter água e o segundo, a conter leite. Para isso, e necessário um terceiro copo que recebe, por exemplo, o conteúdo do primeiro copo e, então, este primeiro copo pode receber o conteúdo do segundo para, então, o segundo receber o conteúdo do terceiro.
Complexidade do algoritmo
A linha 1, tem um for. Lembrando que um for tem embutido uma variávei 'i' que é inicializada 1 vez apenas. Uma condição de parada que é executada 'n+1' vezes, e um incremento, executado 'n' vezes.
A linha 2, é uma atribuição de valor a uma variável que, por estar dentro do for, também é executada 'n' vezes.
Na terceira linha, vem um segundo for. a variável 'j' deste, é executada 'n' vezes e a condição deste é executada: (n-1) + (n-2) + ... + (n-(n-1)) + n. Conforme abaixo:
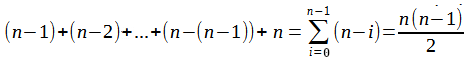
A condição do IF que vem logo após o for, também executa 'n' vezes. Logo, o que influi mais no tempo de execução, é mesmo o for interno. Então, o cálculo do tempo de execução fica conforme abaixo:
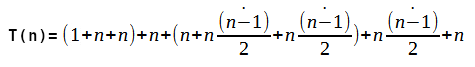
Logo,
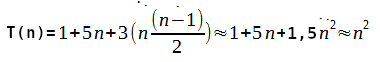
Feito isto, a ordem de crescimento que representa a complexidade do algoritmo é em torno de θ(n²). Isto vale tanto para o pior caso, quanto para o melhor. Mas, por que?
No caso de o vetor já está ordenado previamente, as condições das linhas 5 e 7 sempre são falsas e, ainda sim, neste caso, as condições dos fors e incrementos, bem como as condições das linhas 5 e 7, são exetutadas em todas as iterações. Logo, o tempo de execução do conteúdo dos ifs torna-se pouco expressivo e, ainda assim, o termo do cálculo de complexidade de maior ordem se aproxima de n².
Em se tratando de complexidade de algoritmos, deve ser levado mais em conta o termo de maior ordem no calculos.
Exemplo de implementação em C
Para reforçar o aprendizado sobre a implementação do selection sort, preparei um programinha escrito em C que pode ser baixado logo abaixo:
Link: selectionsort.c
Finalizando
Esse foi o primeiro artigo sobre algoritmos de ordenação. O próximo, abordará a ordenação por intercalação que utiliza a técnica de divisão e conquista: O mergesort.
Então, até o próximo
Inspirado em
Cormen. H. Thomas et. al, 2002 - Algoritmos teoria e prática - 2 ed. Rio de Janeiro - RJ, Brasil, 2002
