Introdução ao cálculo diferencial
No ensino médio, estudamos funções, trigonometria e geometria analítica. Essas partes da matemática são relativamente simples de se dominar. Mas, há uma outra disciplina da matemática que é chamada de cálculo diferencial e integral. Essa disciplina depende das disciplinas de matemática que estudamos no segundo grau e, geralmente, é ensinada em cursos superiores de engenharia e computação. Portanto, este artigo tem por objetivo abordar as funções derivadas, que são componentes do cálculo diferencial, através de uma introdução. Será mostrado também sobre uma das aplicações da derivada: O problema da velocidade relacionado ao da tangente.
Para entender a derivada, é necessário compreender bem sobre funções e o estudo da reta. Para fácil compreenção do conteúdo desse artigo, o leitor deve estar familiarizado com conceitos como: equação da reta, coeficiente angular, pontos no plano cartesiano, conceitos básicos de funções e noção intuitiva de limites de funções. Se você não domina todas essas partes da matemática, não se preocupe! Tentarei esclarecer sobre esses assuntos também.
Então, para começar, vamos entender qual a relação entre a função derivada, o problema da tangente e a equação da reta. Bom, o problema da tangente está ilustrado a seguir, mas antes, veja uma representação de uma reta secante:
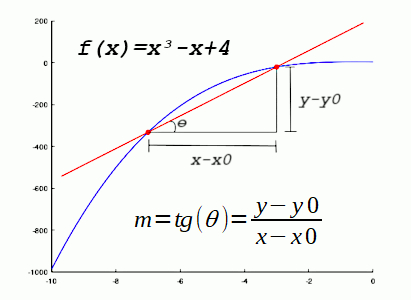
Na figura acima, perceba que a reta secante é a pintada de vermelho. Ela é secante a curva: f(x)=x³+x-4, passando pelos pontos (x0,y0) e (x,y). O coeficiente angular da reta é representado por ɑ e é igual a tangente do ângulo Ɵ. Dado isto, podemos conjecturar pela fórmula do coeficiente angular mostrada na figura acima que a fórmula da equação da reta que passa por dois pontos quaisquer é conforme a ilustrada abaixo:
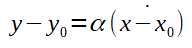
A equação da reta tangente a uma curva é um pouco mais complicada que é a equação da reta secante. Por exemplo, a reta tangente a uma curva é tangente em, não dois pontos quaisquer pertencentes a curva, mas em apenas um. Veja a figura abaixo:
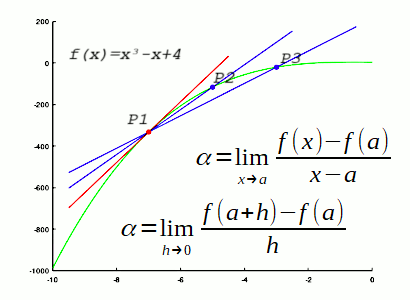
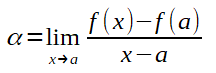
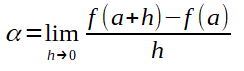
Perceba que a primeira fórmula pode ser comparada com a fórmula do coeficiente angular da equação de uma reta secante. Por exemplo, perceba que o y foi substituido por f(x) e o y0 foi substituido por f(a) e o x0 foi substituido por a. Perceba o limite expresso na fórmula. Foi utilizada a palavra lim para especificar que, para a fórmula da equação da reta ser adaptada para o calculo da função da reta tangente, foi necessário, na fórmula 1, o x tender para a, e na fórmula 2, o h tender para zero. A fórmula 2 foi obtida a partir da fórmula 1, isto é, o x-a foi substituído por h, logo, a+h é igual a x.
A fórmula da equação derivada de uma função, pode ser utilizada para calcular o coeficiente angular da reta tangente a qualquer ponto pertencente a função. Mas, você pode estar se perguntando: e para que isso serve? Bom, a derivada tem diversas aplicações. Uma das mais comuns é a aplicação no problema da velocidade, onde, por exemplo, se tem uma função que representa o espaço percorrido por um objeto móvel em função do tempo. Uma vez representado este movimento através de uma função, se pode calcular a velocidade em função do tempo e espaço percorrido, determinando-se a função derivada da função de movimento. A taxa de variação em um determinado ponto pertencente a função de movimento, é o coeficiente angular da reta tangente a tal ponto. Ou seja, é a variação do espaço dividido pela variação de tempo naquele ponto.
Para compreender melhor a aplicação da derivada no problema da velocidade, pense o seguinte: Qual a fórmula para se calcular a velocidade média de um objeto em movimento? É a seguinte:
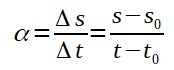
Então, repare no quanto a fórmula se parece com a fórmula da equação da reta secante. Onde, apenas, foi substituído o y por s e o x por t. Veja o exemplo abaixo:
EXEMPLO: Calcule a velocidade de um carro em movimento quando o mesmo atinge um ponto à exatamente 25Km da origem, sendo que, sua função de movimento com t em horas é: f(t)=t²
Resposta: Sabemos que f(t) é igual a 25Km, logo, t² é igual a 25, já que f(t)=t². Então, podemos calcular t em função de f(t) para encontrar em quanto tempo o carro percorreu 25km. Logo,
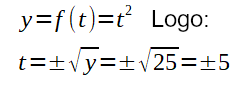
Como o tempo gasto é um valor positivo, o -5 não nos interessa, mas sim, o 5 positivo.
Agora, devemos calcular a função derivada conforme mostrado a seguir:
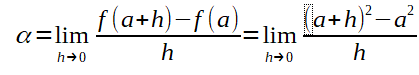
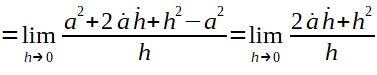
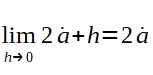
Após calculada a derivada, basta aplicá-la para encontrar a velocidade no ponto a 25Km da origem. Ou seja, Temos f'(t) que é a função derivada igual a 2*t. Então, precisamos calcular qual o coeficiente angular (derivada no ponto P{5,25}) que representa a velocidade do carro em t igual a 5. Então, veja a solução mostrada abaixo:
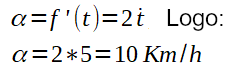
Veja a reta tangente ao ponto (5,25) ilustrada na imagem abaixo:
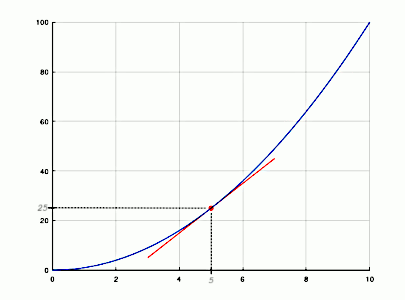
O gráfico da figura acima mostra que, após 5 horas, o carro percorre 25Km, sendo que, sua velocidade não é constante, mas sim, crescente conforme a fórmula f(t)=t². Para calcular a velocidade em outro ponto da função, basta aplicar a mesma fórmula da função derivada encontrada. Por exemplo, veja abaixo o cálculo para t=10horas:
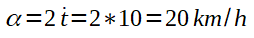
Ou seja, o carro percorre 100km após 10 horas de movimento e, após esse tempo, sua velocidade é de 20km/h.
Obs: para o calculo da derivada, há um meio muito mais simples de calcular. Por exemplo: para calcular a derivada de x² é só seguir a fórmula abaixo que já há provas matemáticas de que a mesma se aplica ao calculo de derivadas de termos exponenciais. Veja abaixo:
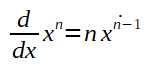
Logo,
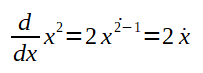
A notação utilizada nos exemplos acima tem o mesmo significado que o f'(x).
E chegamos ao final do artigo sobre cálculo diferencial. No próximo, pretendo escrever sobre limites de funções ou sobre outra aplicação da derivada: O cálculo dos máximos e mínimos locais de uma função. Há muito sobre o que escrever quando o assunto é cálculo diferencial e integral. O que foi mostrado aqui é apenas uma pequena introdução ao cálculo diferencial.
Se gostou do conteúdo, deixe um comentário ou entre em contato pelo e-mail: italoherbert@outlook.com.
Até a próxima!
