Rotação de um polígono 2D
Você já se perguntou como que os programas gráficos oferecem recursos para rotação, translação e escala de formas geométricas? Pois é, existe um modo. Esse artigo visa esclarecer sobre o desenho e rotação de uma simples forma geométrica: Um polígono quadrado. O aplicativo desenvolvido, e mostrado aqui seu código fonte, permite a rotação da forma geométrica com a aplicação da transformação geométrica de rotação. Vale ressaltar que os conceitos expostos aqui servem para a rotação de qualquer polígono, seja quais forem suas coordenadas e número de lados.
Bom, para começar, vamos compreender como representar uma forma geométrica compatível com as transformações geométricas. Isto é, que se possa rotacionar, transladar, escalar, etc. Para tanto, a forma geométrica (em 2D) deve ser representada por uma estrutura de vértices e arestas.
Então, vamos lá! Vamos supor que o quadrado tenha lado de L pixels. Então podemos calcular os vetores de coordenadas relativas ao ponto (0,0), de modo que se possa, após as transformações geométricas, deslocar para, por exemplo, o centro da tela. Veja o cálculo das coordenadas dos vetores abaixo:
x1 = -L/2;
x2 = L/2;
x3 = L/2;
x4 = -L/2;
y1 = -L/2;
y2 = -L/2;
y3 = L/2;
y4 = L/2;
Logo: V1 = (-L/2,-L/2), V2 = (L/2,-L/2), V3 = (L/2,L/2), V4 = (-L/2,L/2).
Além de ter representado seus vértices, a forma geométrica também deve ter associada uma representação das arestas. Então, vamos calcular as arestas do quadrado representado em 2D pelos vértices V1, V2, V3 e V4. São quatro arestas, veja abaixo
A1 = (V1, V2);
A2 = (V2, V3);
A3 = (V3, V4);
A4 = (V4, V1);
Isso conecta os vértices que formam o quadrado.
Rotacionando a forma
Para rotacionar uma forma qualquer, representada em 2D em uma estrutura de vértices e arestas, devemos calcular, para cada vértice da forma, as coordenadas do vértice resultante. Veja a figura abaixo:
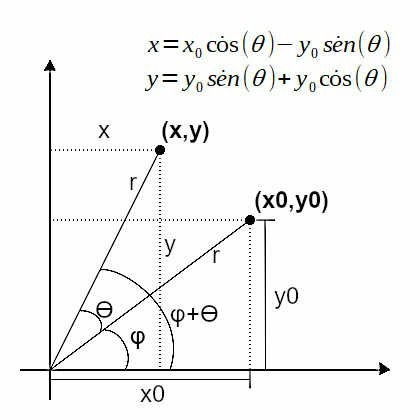
Queremos calcular o ponto (x,y) com base no ponto (x0,y0) e o angulo Ɵ. Repare nas fórmulas para se determinar o x e o y correspondentes ao resultado da rotação do vértice de coordenadas x0 e y0. Quando estiver estudando as fórmulas volte a figura acima sempre que achar necessário. Então, veja abaixo o cálculo para se chegar a tais fórmulas:
Perceba na figura acima que:
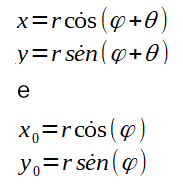
Assuma também a seguintes propriedades:
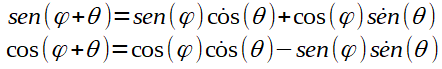
Substituindo:
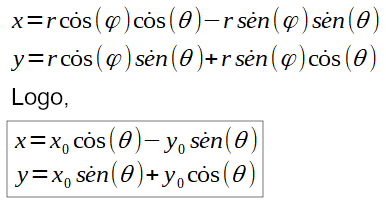
Translação e escala
Para transladar, basta adicionar o valor da translação pertinente a cada variável do vertice, e para escalar, basta multiplicar os fatores pelas variáveis do vertice. A translação e escala são muito mais simples de aplicar do que a rotação. Veja as fórmulas abaixo:
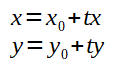

O programa
Veja abaixo o programa que desenha, primeiro, o quadrado sem rotação, de cor cinza, e depois, o quadrado de cor branca rotacionado a um ângulo de 30 graus.
package quadrado2d;
import java.awt.Color;
import java.awt.Dimension;
import java.awt.Graphics;
import javax.swing.JFrame;
import javax.swing.JPanel;
public class Forma2DPainel extends JPanel {
public Forma2DPainel() {
super.setBackground( Color.BLACK );
super.setPreferredSize( new Dimension( 640, 480 ) );
}
public void paintComponent(Graphics g) {
super.paintComponent( g );
this.desenhaQuadrado( g, 200, 0, Color.DARK_GRAY );
this.desenhaQuadrado( g, 200, Math.toRadians( 30 ), Color.WHITE );
}
private void desenhaQuadrado( Graphics g, int l, double ang_rot, Color corArestas ) {
// CÁLCULO DOS VERTICES COMO VETORES
// RELATIVOS AO CENTRO DA TELA
int x1 = -(l/2);
int x2 = l/2;
int x3 = l/2;
int x4 = -(l/2);
int y1 = -(l/2);
int y2 = -(l/2);
int y3 = l/2;
int y4 = l/2;
int[] P1 = { x1, y1 };
int[] P2 = { x2, y2 };
int[] P3 = { x3, y3 };
int[] P4 = { x4, y4 };
int[][] A1 = { P1, P2 };
int[][] A2 = { P2, P3 };
int[][] A3 = { P3, P4 };
int[][] A4 = { P4, P1 };
int[][] vertices = { P1, P2, P3, P4 };
int[][][] arestas = { A1, A2, A3, A4 };
// ROTAÇÃO DOS VÉRTICES (Ângulo em Radianos)
double theta = ang_rot;
for( int[] v : vertices ) {
int x0 = v[0];
int y0 = v[1];
int x = (int) ( x0 * Math.cos( theta ) - y0 * Math.sin( theta ) );
int y = (int) ( x0 * Math.sin( theta ) + y0 * Math.cos( theta ) );
v[0] = x;
v[1] = y;
}
// CÁLCULO DAS COORDENADAS ABSOLUTAS DOS VÉRTICES
int larguraTela = super.getWidth();
int alturaTela = super.getHeight();
for( int[] v : vertices ) {
v[0] = ( larguraTela / 2 ) + v[0];
v[1] = ( alturaTela / 2 ) + v[1];
}
// DESENHO DAS ARESTAS
for( int[][] aresta : arestas ) {
int lx1 = aresta[0][0];
int ly1 = aresta[0][1];
int lx2 = aresta[1][0];
int ly2 = aresta[1][1];
g.setColor( corArestas );
g.drawLine( lx1, ly1, lx2, ly2 );
}
// DESENHO DOS VÉRTICES E COORDENADAS
for( int[] vertice : vertices ) {
int x = vertice[0];
int y = vertice[1];
g.setColor( Color.BLUE );
g.fillArc( x-5, y-5, 10, 10, 0, 360 );
g.setColor( Color.WHITE );
g.drawString( "("+x+","+y+")", x+5, y-10 );
}
}
public static void main(String[] args) {
Forma2DPainel painel = new Forma2DPainel();
JFrame f = new JFrame( "Desenho de forma 2D" );
f.setDefaultCloseOperation( JFrame.EXIT_ON_CLOSE );
f.setContentPane( painel );
f.pack();
f.setLocationRelativeTo( f );
f.setVisible( true );
}
}
Muito bem, o programa acima, quando executado, desenha o quadrado de 200 pixels de lado na tela. Claro que seria muito mais fácil desenhar o quadrado utilizando o método drawRect ou o método drawPolygon mas, é necessário representar os vértices como vetores relativos porque as transformações geométricas de rotação, translação e escala, devem ser aplicadas a esses vértices para o cálculo dos vertices resultantes de tais transformações. Abaixo o resultado da execução do código acima:
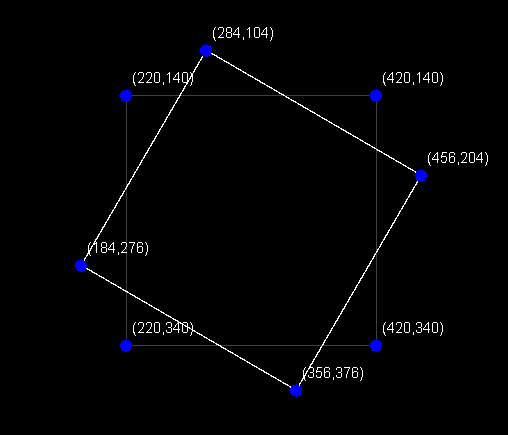
Entenda que, para rotacionar outras formas geométricas, como: triângulo, retângulo e polígono qualquer, uma vez representadas em uma estrutura de vertices e arestas, basta aplicar as transformações aos vértices. Por exemplo, experimente alterar o programa acima (ou fazer outro) para desenhar um polígono rotacionado (diferente do quadrado) que pode ter vários lados e vários vértices.
E assim chegamos ao final desse artigo que ensina como desenhar, em Java, um quadrado rotacionado. Perceba que, os conceitos aqui aprendidos podem ser aplicados em qualquer linguagem de programação com suporte ao desenho de um gráfico. Experimente alterar o programa acima para rotacionar o quadrado em diferentes ângulos e com diferentes tamanhos. Altere os parâmetros passados para o método desenhaQuadrado. e tente desenhar mais que dois quadrados rotacionados na tela!
