Introdução ao perceptron MLP
Cálculos aprendidos em: MEDIUM.COM
O perceptron multi-camadas ou (MLP – MultiLayer Perceptron), é um algoritmo de redes neurais artificiais que tem diversas aplicações. Por isso, esse artigo trata do assunto, descrevendo o algoritmo e visando facilitar o aprendizado do mesmo. Um dos problemas clássicos de aplicação do MLP é no problema da operação booleana XOR. Trata-se de um problema que a aplicação do perceptron simples (de uma única unidade de processamento - neurônio) não resolve. Mais adiante será explicado o porquê. No decorrer desse artigo, será abordado detalhes do MLP, bem como, também, o ajuste dos pesos a cada época de treinamento com a utilização do algoritmo backpropagation, também conhecido como retropropagação do erro. Por último, será disponibilizado para download, o código fonte de um projeto do MLP aplicado ao problema do XOR!
O perceptron simples
O perceptron simples é o modelo de rede neural artificial mais básico e tem apenas uma unidade de processamento (O neurônio) que recebe sinais de entradas e realiza uma soma ponderada envolvendo pesos que ligam cada entrada ao neurônio, e gera uma saída. Tais pesos são ajustados a cada iteração de treinamento do perceptron dado o erro obtido na iteração corrente. Veja abaixo uma imagem que ilustra o modelo perceptron:
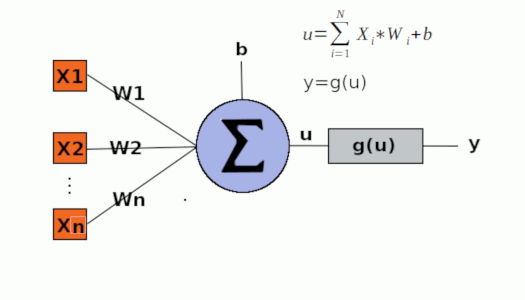
Perceba na imagem acima que, durante cada iteração do algorítmo, os dados de entrada (sinais) são multiplicados por diferentes pesos, os resultados dessas multiplicações são somados para compor um somatório e, depois, o somatório obtido é somado com o valor do bias para esse resultado compor o potencial de ativação. Uma função de ativação é utilizada para, tomando como entrada o potencial de ativação, gerar uma saída. A saída, após calculada, é comparada com a saída desejada para o calculo do erro e, caso o erro seja diferente de zero (ou menor que um limiar definido), os pesos são ajustados de modo a aproximar a próxima saída obtida na próxima iteração da saída desejada. Para tanto, é necessário determinar a parcela de influência que cada peso tem na saída obtida para, então, dado o erro calculado, ajustar tais pesos de acordo com sua parcela de influência no erro resultante. Como o erro é calculado para os pesos serem ajustados conforme a comparação das saídas com as saídas desejadas, o perceptron é um algoritmo de treinamento supervisionado.
O neurônio biológico
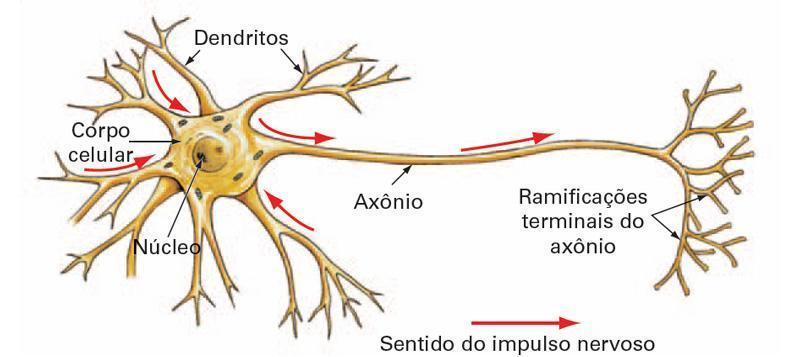
De modo bastante superficial, a imagem abaixo ilustra o funcionamento de um neurônio biológico, levando em conta conceitos como: dentritos, axónios, cuja conexão forma uma sinápse, e corpo celular, que realiza a soma dos sinais propagados por outros neurônios e recebidos por ele através de seus dentritos.
http://deeplearningbook.com.br/o-neuronio-biologico-e-matematico/
Perceba na ilustração acima que as sinapses são ligações, consideradas ligações sinápticas, entre axônios de alguns neurônios e dentritos de outros neurônios. O núcleo do corpo celular, ao receber esses sinais (pulsos elétricos ou nervosos), "soma-os", gerando assim um novo pulso nervoso que é propagado por seu axônio ligado a dentritos de outros neurônios.
Nosso cérebro tem a capacidade de reforçar ligações sinápticas conforme funciona sua rede de neurônios e, inclusive, nosso aprendizado (cognição) está nessas ligações sinápticas que ligam, também, nossos sentidos, através de: nervos sensitivos (para olhos, ouvidos, pele, etc) e nervos motores (para nossos músculos). Pulsos elétricos transmitidos por nossos nervos motores tornam possível os movimentos de nossos membros, como: braços e pernas, bem como, nossos lábios e coração. Em analogia com o modelo matemático, nossos nervos sensitivos recebem sinais de entrada que têm influência em nosso aprendizado e cognição e os nervos motores propagam sinais de saída, também detectados por nosso sistema perceptual (sensitivo), já que o nosso movimento, quando percebido por nosso cérebro também pode gerar aprendizado.
O potencial de ativação do neurônio matemático, em analogia com o funcionamento do neurônio biológico, é a "soma" dos sinais transmitidos entre células nervosas (neurônios), recebidos pelo núcleo de um neurônio e, após tal neurônio somar (ou processar) os sinais recebidos, propaga um novo sinal resultante dessa "soma", para outros neurônios.
O perceptron multicamadas (MLP)
O MLP permite resolver uma limitação do perceptron simples: a incapacidade de diferenciar classes não linearmente separaveis. Isso é possível com o perceptron MLP porque o mesmo pode ser organizado em várias camadas de neurônios, que podem variar conforme a aplicação. Um exemplo clássico de problema não linearmente separavel e que pode ser resolvido com a aplicação do MLP é o da operação booleana XOR. Veja a imagem abaixo:
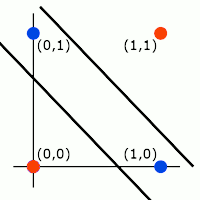
Perceba na imagem acima que não é possível traçar apenas uma linha para separar as saídas em duas as classes. Por isso, o problema não é linearmente separável!
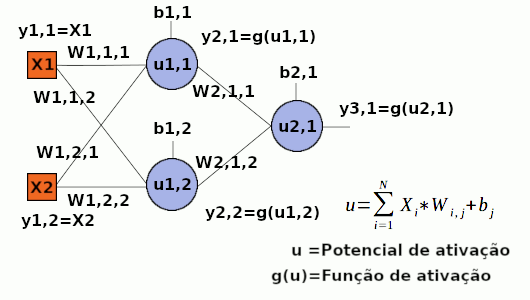
O MLP é um algoritmo de redes neurais artificiais que agrupa os neurônios em camadas, onde, cada neurônio de cada camada é conectado a todos os neurônios da camada seguinte. O que permite que um sinal de entrada seja propagado até a última camada (a camada de saída). Após a rede gerar uma saída, ela é comparada com a saída desejada (Isso porque o MLP é um algoritmo de RNA supervisionado) e, assim, é calculado o erro que se refere a diferença entre a saída obtida e a desejada. Apos calculado o erro, ele deve ser retropropagado, isto é, propagado da última camada até a primeira, de modo que, é determinada a influência de cada peso no erro calculado, para que cada peso seja ajustado para diminuir o erro em iterações (ou época) futuras. Mas uma questão que pode surgir é: Como calcular a influência de cada peso no erro? E como ajustar os pesos de modo a diminuir o erro e aproximar a saída obtida da desejada? Essas perguntas serão respondidas no decorrer desse artigo. Por enquanto, veja a imagem abaixo:
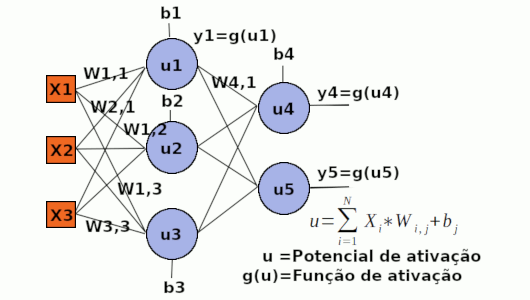
Na figura acima se pode observar as entradas, representadas com X, os pesos como W, os potenciais de ativação como u, os biases como b, as funções de ativação g(u) e as saidas como y. Obs: Para aplicação do MLP ao problema do xor, as entradas X devem ser normalizados, isto é, entre 0 e 1, já que há apenas duas classes nessa aplicação: falso (0) e verdadeiro(1) dados os valores binários recebidos como entrada
A inicialização dos pesos e biases
A inicialização dos pesos e biases, pode contribuir para diminuir o número de iterações necessárias para se atingir saídas próximas o suficiente das saídas desejadas. No entanto, dependendo da aplicação, principalmente em problemas não linearmente separáveis, torna-se muito difícil se determinar os pesos e biases iniciais ideais. Então, geralmente se recorre a técnicas como, por exemplo, sortear valores em torno de zero, conforme um ráio como limiar. Por exemplo, se o raio for 0.1, sorteia-se valores entre -0.1 e 0.1 para cada peso e cada bias. Vale esclarecer também que, o raio de inicialização dos pesos pode ser diferente do raio de inicialização dos biases, isso para que cada bias não se torne, apenas, mais um peso na rede. A taxa de aprendizado (que será vista mais adiante) também pode variar para pesos e para biases.
O potencial de ativação
A fórmula do potencial de ativação para o MLP é a mesma do percéptron simples, sendo que, no MLP, para neurônios cuja camada anterior não é a camada de entradas, as entradas são as saídas dos neurônios anteriores. Veja a fórmula para o cálculo do potencial de ativação logo abaixo:
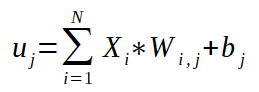
Como já dito, na fórmula acima, as entradas Xs podem ser os sinais submetidos a rede ou a saida de neuronios que são entradas de outros neurônios. O bias b está associado aos neurônios, isto é, cada neurônio tem um bias e gera um potencial de ativação u que corresponde a soma ponderada das entradas pelos devidos pesos. Após o cálculo da soma ponderada, o resultado obtido é somado ao bias.
A função de ativação
Uma função bastante utilizada para função de ativação em MLP onde se deseja uma classificação entre 0 e 1, é a sigmoide porque ela retorna valores entre 0 e 1, que representam uma saida y. Como a saída da função sigmoide está entre 0 e 1, ela já sai normalizada. Por isso, também, a utilidade da função nesse tipo de aplicação. No caso do problema do XOR se quer que, apos os sinais de entrada submetidos a rede, as saidas obtidas sejam valores entre 0 e 1. Veja abaixo a plotagem do gráfico da sigmoide para x no intervalo de -10 a 10:
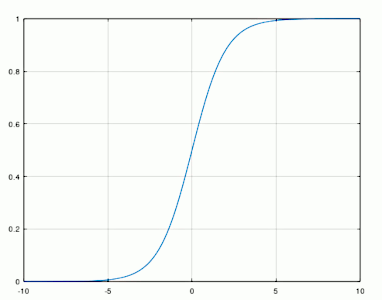
Perceba que a saída y da função sigmoide está no intervalo [0,1] e a entrada x está entre [-10, 10]. Perceba também que a saída se aproxima de um e permanece um após o 5 e se aproxima de zero e permanece zero antes do -5. Logo, é considerável que, se o potencial de ativação calculado tiver valor maior que 5, a saída da aplicação da função de ativação sigmoide é 1, se tiver valor menor que -5, a saída é zero.
DEEPLEARNINGBOOK - Função de ativação
Erro total
Antes de ajustar os pesos da rede, é necessário calcular o erro total que corresponde ao somatório do quadrado da diferença entre a saida desejada e a obtida. O quadrado da diferença elimina resultados negativos da subtração. Veja o cálculo do erro total ilustrado na fórmula abaixo:
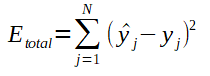
Atualização dos pesos e biases
Para atualizar os pesos e biases devem ser utilizadas as fórmulas abaixo:
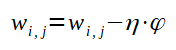
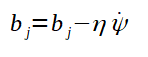
Para a atualização dos pesos, cada peso recebe o valor dele mesmo menos o produto da taxa de aprendizado pelo fator gradiente. O menos na fórmula corresponde a tentativa de direcionar o gradiente para o mínimo local, dado que, o gradiente encontrado pelo devido cálculo aponta para o máximo local. A direção do mínimo local é utilizada visando-se diminuir o erro. É importante frizar que, para o ajuste dos pesos, deve-se utilizar um algoritmo conhecido como backpropagation ou retropropagação que será detalhado mais adiente. A atualização do bias é análoga a dos pesos, sendo que, é calculado um novo gradiente para o bias a ser atualizado.
A taxa de aprendizado é um fator de multiplicação que visa contribuir com a aproximação do valor do peso ao valor ideal para que ele, junto dos demais, possam aproximar as saídas obtidas das desejadas. Isso, porque a taxa de aprendizado é multiplicada pelo valor do gradiente que serve de direção para o ajuste dos pesos.
Backpropagation
Após o cálculo do erro, se pode retropropagá-lo da camada de saida até a camada de entrada, ajustando os pesos que conectam essas camadas. Uma consideração importante é que o ajuste dos pesos visa diminuir o erro total obtido. Portanto, é importante determinar qual a parcela de culpa (influência) que tem um determinado peso no erro total para que o ajuste do peso possa diminuir o erro. Outra coisa que é necessário considerar é que, após determinar o quanto o peso tem influência no erro, deve ser determinada a direção em que o peso deve ser ajustado para que o ajuste realmente diminua o erro, isto é, se é necessário acrecentar ou diminuir do valor do peso. Para o ajuste ser correto, é necessário o cálculo do vetor gradiente. O vetor gradiente, quando calculado, aponta para a direção cujo caminho leva ao máximo local de uma função (ou superfície). Ou seja, basta determinar o vetor gradiente que se sabe qual a direção para se chegar ao mínimo local. Como o vetor gradiente aponta para o caminho que leva ao máximo local, o vetor que aponta para o mínimo local é o gradiente multiplicado por -1. A necessidade de buscar o mínimo local se deve ao fato de que a intenção é minimizar o erro. Claro, o ideal seria calcular o mínimo global da função, mas, quando o gradiente atinge um mínimo local, a derivada de tal ponto é 0 e, por isso, esse gradiente não aponta para nenhuma direção, impedindo que, o gradiente direcione para o minimo global.
Ajuste dos pesos ligados a camada final
Para o calculo do gradiente, basta derivar as funções de que se deseje calcular o mínimo local. O gradiente é calculado por derivada parcial que corresponde a taxa de variação em relação ao parâmetro de entrada da função. Tal taxa de variação, quando aplicada a uma função que recebe o peso como uma de suas entradas, representa a culpa do mesmo no resultado da função. Seguindo a figura da MLP ilustrada atrás (volte a esta figura sempre que necessário para sua compreenssão), para calcular a parcela de influência no erro total do peso W4,1, que corresponde a taxa de variação entre o erro total e W4,1 basta calcular o gradiente conforme abaixo:
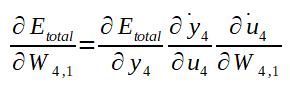
Perceba que, para calcular o gradiente, foi necessário quebrar o cálculo da derivada em três, com aplicação da regra da cadeia. Essa divisão em três partes se dá pelo fato de a saída y ser calculada em função do potencial de ativação u, o potencial de ativação u ser calculado em função da soma ponderada das entradas multiplicadas pelos pesos Ws somados ao bias do neurônio em questão.
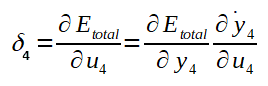
Logo:
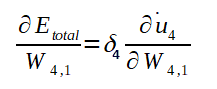
Outras fórmulas importantes que serão utilizadas mais a frente:
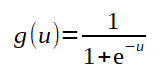
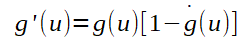
O seguinte link é boa referência sobre a função matemática sigmoide: WIKIPEDIA - Função sigmoide
O cálculo da derivada da sigmoide não é trivial, por isso, não será detalhado aqui. Abaixo os calculos de cada parte do calculo do gradiente:
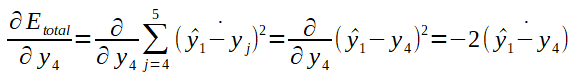
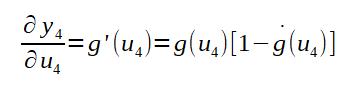
Como g(u4)=y4, poderia-se substituir na fórmula abaixo. Mas, por questões de comparação com cálculos feitos mais a frente, decidi deixar o cálculo final do Delta 4 como segue abaixo, isto é, substituindo de acordo com os resultados das fórmulas anteriores:
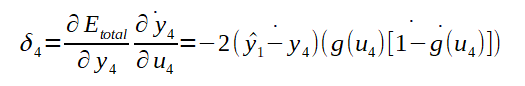
Para o cálculo da derivada parcial de u4 em relação a W4,1, se pode utilizar o somatório com índices variando de 1 a 2, que são os dois possíveis índices para o segundo índice do vetor de pesos, já que os pesos da última camada são conectados a 2 neurônios de saída. Veja abaixo o cálculo:
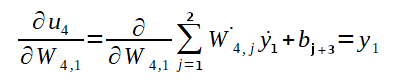
Logo:
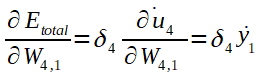
A fórmula de ajuste do peso W4,1:
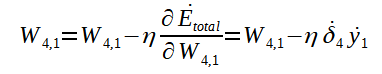
Ajuste genérico
Agora, perceba o seguinte: o cálculo para o ajuste dos outros pesos que ligam os neurônios da penúltima camada aos da última pode ser feito de modo análogo ao do peso W4,1. Veja a fórmula genérica abaixo:
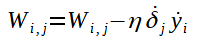
Você deve entender que, na fórmula acima, o i varia conforme o número de neurônios da penúltima camada e o j varia conforme o número de neurônios da última camada.
Ajuste dos biases da ultima camada
O calculo do ajuste dos biases também é de forma análoga ao ajuste dos pesos. Após calculado, veja o gradiente para o bias b4:
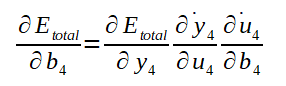
Mais uma vez, acima, foi aplicada a regra da cadeia!
Como:
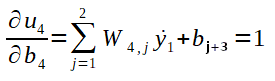
Então:
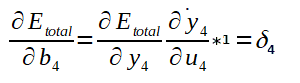
Ajuste de b4:
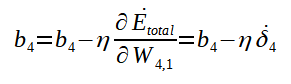
Ajuste genérico
Assim como a fórmula genérica para o ajuste dos pesos da última camada, se pode generalizar também o ajuste dos biases da última camada. Veja a fórmula genérica abaixo:
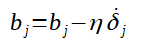
Você deve entender que, na fórmula acima, o j varia conforme o número de neurônios da última camada.
Ajuste dos pesos das camadas anteriores
Agora que calculamos o ajuste para o peso W4,1 e o ajuste do bias b4, bem como as fórmulas genéricas, vamos calcular o ajuste de um peso e de um bias da segunda camada de neurônios: O peso W1,1 e o bias b1. Segue a fórmula do gradiente para W1,1:
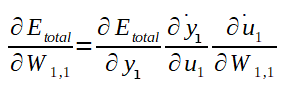
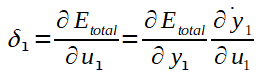
Logo:
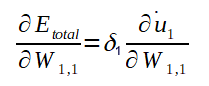
Note que não conhecemos ainda a derivada parcial do Erro total em relação a saida y1 (necessário no cálculo do Delta 1) e, como o valor do y1 é propagado para todos os neurônios da camada de saída, a fórmula para calculá-la também envolve todos os potenciais de ativação e saídas da camada de saída. Pois, até este ponto, o algoritmo já deve ter calculados todos os ajustes dos pesos que ligam a camada intermédiária a ultima camada de neurônios. Portanto, podemos calcular a derivada parcial do Erro total em relação a y1 como segue:
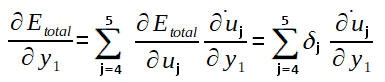
Considere que:
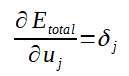
E,
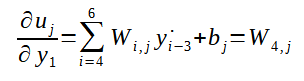
Logo:
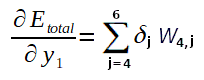
Abaixo o calculo para a derivada parcial de y1 em relação a u1:
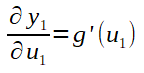
Perceba que para o cálculo de g'(u1), se pode utilizar a fórmula mostrada anteriormente para o cálculo da derivada da função de ativação sigmoide.
Portanto, g'(u1)=g(u1)*[1-g(u1)].
Logo,
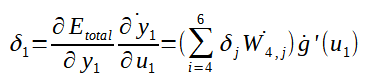
Agora falta pouco! Basta calcular a derivada parcial de u1 em relação a W1,1. Perceba que o número de entradas são 3 e os primeiros índices dos pesos que conectam cada entrada a cada neurônio da camada intermediária varia de 1 a 3. Logo, o cálculo pode ser feito conforme a fórmula abaixo:
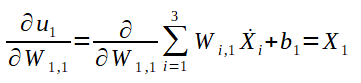
E então, chegamos a fórmula do gradiente para W1,1. Veja abaixo:
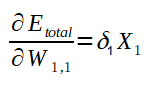
Ajuste genérico
Agora, perceba o seguinte: o cálculo para o ajuste dos outros pesos que ligam os neurônios da primeira camada aos da segunda pode ser feito de modo análogo ao do peso W1,1. Veja a fórmula genérica abaixo:
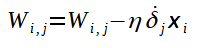
Você deve entender que, na fórmula acima, o i varia conforme o número de neurônios da primeira camada e o j varia conforme o número de neurônios da segunda camada.
Ajuste dos biases da camada intermediária
O calculo do ajuste dos biases também é de forma análoga ao ajuste dos biases da ultima camada. Após calculado, veja o gradiente para o bias b1 e a expressão de ajuste dele:
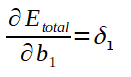
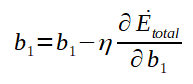
Ajuste genérico
Assim como a fórmula genérica para o ajuste dos pesos das camadas primeira e segunda, se pode generalizar também o ajuste dos biases da segunda camada. Veja a fórmula genérica abaixo:
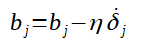
Você deve entender que, na fórmula acima, o j varia conforme o número de neurônios da segunda camada.
O problema do XOR
O perceptron simples tem uma limitação: não suporta a aplicação a operação booleana XOR, cujos possíveis resultados para duas entradas binárias, formam dois grupos não linearmente separaveis. Diferente do perceptron simples, o perceptron multicamadas tem suporte para distinção de classes não linearmente separáveis. Por isso, desenvolvi um programa em Java que treina um MLP para o calculo da operação booleana XOR. A rede tem: 2 entradas que podem assumir valores em binário, uma camada de neurônios intermediária com 2 neurônios e uma camada de saída com apenas 1 neurônio cuja saída pode assumir valores entre 0 e 1. Claro, busca-se, com o treinamento da rede, se conseguir aproximar dos zeros e uns correspondentes as saídas de cada conjunto de entradas. O programa tem apenas três classes Java, e uma classe principal. Veja abaixo a arquitetura da rede:
Configuração da rede:
- Entradas: {0,0}, {0,1}, {1,0}, {1,1}
- Saídas desejadas: {0}, {1}, {1}, {0}
- Número de camadas: 3
- Camada (1): 2 entradas. Ex: {0, 1}
- Camada (2): 2 neurônios intermediários
- Camada (3): 1 neurônio de saída. Ex de saída: {0,9998} - "Quase 1"
- Número de épocas (iterações): 10000
- Taxa de aprendizado: 0.5
- Pesos iniciais: sorteados entre -0.1 e 0.1
- Biases iniciais: sorteados entre -1 e 1
Resultados obtidos
Com 10000 épocas foi obtido o resultado mostrado abaixo:
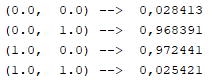
O resultado encontrado foi em torno do esperado após 10000 épocas. Trata-se de aproximações dos resultados desejados. Após 500000 épocas o resultado já estaria mais próximo dos desejados. Veja abaixo o resultado para 10000000 épocas:
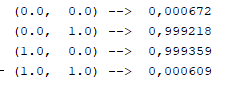
Vale salientar que, para o problema do XOR, o custo computacional de se executar 10000000 épocas é pequeno. No meu computador, foi em torno de 2 ou 3 segundos. Já para MLP aplicada a processamento de imagens onde cada píxel tem três valores RGB ou quatro valores RGBA, em uma imagem de 32x32 pixels representados em RGB, seriam 32 x 32 x 3 sinais de entrada, conectados a muitos neurônios organizados em um número de camadas de acordo com a aplicação. Então, nesse caso, o custo computacional de 10000 iterações pode ser alto. Por isso, as aproximações dos resultados desejados, mesmo que, em torno de 90% a 95% de precisão, são bons resultados e, geralmente, são assumidos como resultados finais e satisfatórios.
Vale esclarecer que há uma variação do MLP que pode ser aplicada a classificação/reconhecimento de padrões em imagens. Me refiro as Redes Neurais Convolucionais, onde, se busca criar duas ou três camadas de processamento que resulta nos dados de entrada normalizados com características extraidas e tamanho diminuido. Geralmente, para aplicações em imagens, busca-se representar as imagens de entrada em tons de cinza ou mesmo com limiar binário (apenas 2 cores).
Abaixo o download do projeto MLP_XOR:
Download do projeto MLP_XOR: clique aquiBaixe o código, ele está comentado. Tente compreendê-lo e crie sua própria versão! Aproveite e implemente o sorteio disperso dos valores iniciais dos pesos e biases!
E este é o fim do artigo em que foi bastante focado o algoritmo de retropropagação de erro: o backpropagation. Além de conceitos mais simples como o perceptron de um único neurônio.
Se você gostou do conteúdo, entre em contato deixando seu comentário ou mandando um e-mail para italoherbert@outlook.com.
Até o próximo!
