Desenhando em Java
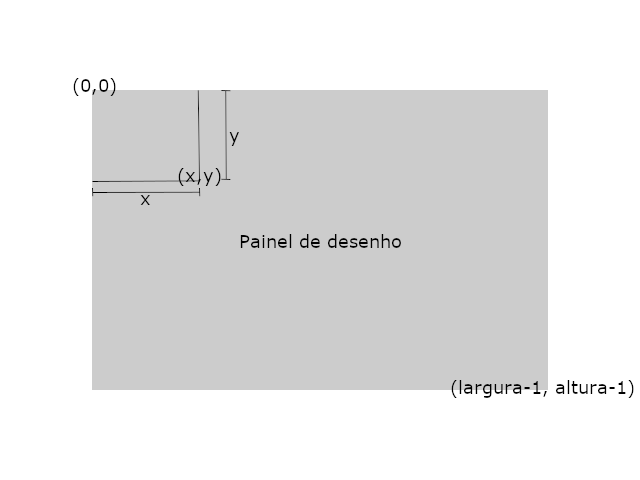
Para desenhar em Java, precisamos lidar com coordenadas semelhantes ao plano cartesiano que aprendemos na escola, sendo que, com coordenadas (0,0) no canto superior esquerdo. Veja a imagem abaixo:
Agora, vamos ao código Java que cria uma simples Janela com um painel de desenho. Para começar, precisamos determinar qual o tamanho da janela e do painel de desenho. Por exemplo, vamos criar uma janela com um painel de desenho de 640px de largura e 480px de altura. Veja o código abaixo
import java.awt.*;
import javax.swing.*;
public class PainelDesenho extends JPanel {
public PainelDesenho() {
Dimension d = new Dimension( 640, 480 ); // cria uma instância da classe Dimension com a largura e altura do painel de desenho
super.setPreferredSize( d ); // informa ao painel de desenho a dimensão (largura e altura) que o painel de desenho deve assumir
}
public void paintComponent( Graphics g ) {
super.paintComponent( g );
g.setColor( Color.BLUE ); // altera a cor de desenho e pintura para AZUL (BLUE em inglês)
g.fillRect( 20, 20, 600, 440 ); // desenha um retangulo azul começando nas coordenadas (20px, 20px) e tendo como largura 600px e altura 440px
g.setColor( Color.BLACK );
g.drawLine( 20, 20, 600, 440 ); // desenha uma linha de cor preta começando nas coordnadas (20, 20) e terminando nas coordenadas (600, 440)
g.setColor( Color.GREEN );
g.drawArc( 40, 40, 560, 400, 0, 360 ); // desenha uma elipse dentro de um retângulo invisível que começa nas coordenadas (40, 40) e
} // tem largura e altura de (560, 400)
public static void main( String[] args ) {
PainelDesenho p = new PainelDesenho(); // instância do painel de desenho
JFrame f = new JFrame(); // Cria a janenal
f.setTitle( "Desenhando em Java" ); // Altera o título da janela
f.setContentPane( p ); // Altera o painel de conteúdo da janela para o painel de desenho
f.setDefaultCloseOperation( JFrame.EXIT_ON_CLOSE ); // define a operação a ser executada quando o usuário fecha a janela. Neste caso SAIR E FECHAR
f.pack(); // comprime a janela para o tamanho do painel de conteúdo mais o tamanho da barra de título da janela
f.setLocationRelativeTo( f ); // centraliza a janela
f.setVisible( true ); // torna a janela visível
}
}
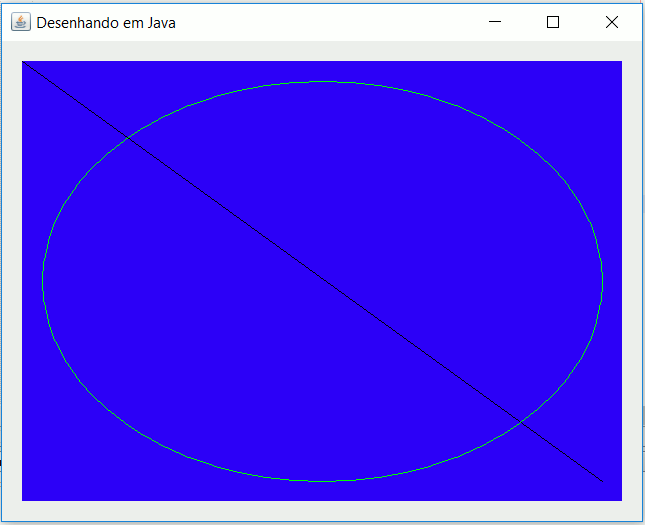
O código acima é simples de entender e está comentado. Com a execução dele, é criada uma janela com algumas formas geométricas desenhadas. Perceba que os códigos de desenho ficam no método "paintComponent". A partir daqui, os exemplos serão voltados apenas para os códigos que ficam no método paintComponent. Logo, utilize o programa acima como modelo para os demais exemplos. Veja abaixo o resultado do código acima:
Algo importante de ser compreendido em se tratando de desenho em uma linguagem de programação, é o cálculo feito com base em variáveis. Isto é, toda forma geométrica pode ser representada por um polígono com vertices e arestas que ligam os vertices, formando assim a forma geométrica. Por exemplo, para desenhar em Java ou outra linguagem, é importante conhecer as dimensões da tela ou painel de desenho, isto é, largura e altura da tela. outra coisa importante de se conhecer é sobre o sistema de coordenadas da biblioteca gráfica utilizada. Em java, o eixo x do plano que representa a tela de desenho cresce de traz para frente, e o eixo y, cresce de cima para baixo, não de baixo para cima como o sistema de coordenadas cartesiano que estudamos na escola. Veja mais adiante, um exemplo de desenho de um polígono de 6 lados iguais, um hexágono.
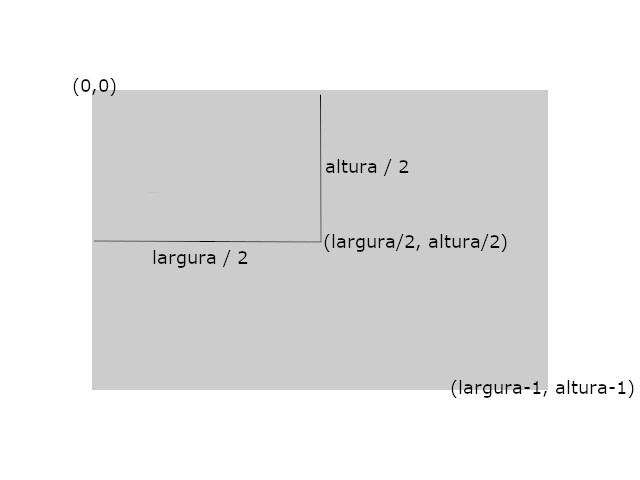
Para o desenho de um hexágono, é necessário, caso queiramos centralizá-lo, conhecer as coordenadas do centro da tela. E, claro, para calcular as coordenadas do centro da tela, é necessário o conhecimento da largura e altura da tela (painel) de desenho. Veja abaixo como determinar as coordenadas do centro da tela:
int centroX = largura_tela / 2;
int centroY = altura_tela / 2;
Veja a imagem abaixo para compreender melhor o porquê das coordenadas centrais serem iguais a metade da largura e metade da altura. Isso, se tomarmos como base as coordenadas (0,0). Perceba que para desenhar o polígono centralizado, tomamos como base as coordenadas do centro da tela, não a coordenada (0,0). O que significa que o centro da tela é relativo as coordenadas (0,0) e o hexágono a ser desenhado terá como coordenadas iniciais as coordenadas do centro da tela.
Agora vamos ao desenho do hexágono! Para desenhar o hexágono, precisamos determinar seus vertices como vetores bidimensionais relativos as coordenadas do centro da tela. Veja o exemplo que ilustra um simples estudo do hexágono:
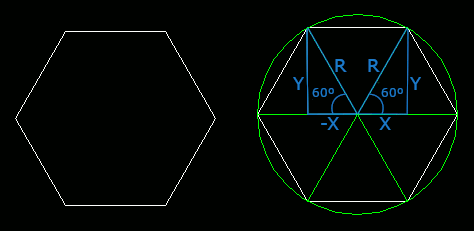
Repare que o hexágono, por ter 6 lados, torna possível parti-lo em 6 pedaços, formando triângulos com ângulo agudo de 60º cada. Então, primeiramente, temos que calcular esse ângulo que corresponde a 60º em radiano. Ou seja 60º é igual a ( PI / 3 ). Repare também que as coordenadas X,Y relativas ao centro da tela de desenho são os catetos dos triângulos formados com ângulo de 60º. Logo, podemos aplicar os seguintes cálculos:
sen( ang ) = cateto oposto / hipotenusa; cos( ang ) = cateto adjacente / hipotenusa; logo, cateto adjacente é igual a X e cateto oposto é igual a Y, as coordenadas procuradas! A hipotenusa é igual ao ráio de do cirtulo que circunscreve o hexágono. Veja: sen( ang ) = y / raio; => y = raio * sen( A ); cos( ang ) = x / raio; => x = raio * cos( A ); para calcular as coordenadas X e Y relativas a um ponto (PX, PY), que pode ser, por exemplo, as coordenadas centrais da tela de desenho, caso queiramos centralizar a forma geométrica desenhada, é só fazer o seguinte: x = px + ( raio * cos( ang ) ); y = py + ( raio * sen( ang ) );
Veja o código fonte abaixo em que são aplicados os cálculos acima:
int larguraTela = super.getWidth();
int alturaTela = super.getHeight();
int centroX = larguraTela / 2;
int centroY = alturaTela / 2;
int raio = 100;
double angulo = Math.PI / 3.0d;
int[] vetorX = new int[ 6 ];
int[] vetorY = new int[ 6 ];
for( int i = 0; i < 6; i++ ) {
double a = angulo * i;
vetorX[i] = centroX + (int)Math.round( raio * Math.cos( a ) );
vetorY[i] = centroY + (int)Math.round( raio * Math.sin( a ) );
}
g.setColor( Color.WHITE );
g.drawPolygon( vetorX, vetorY, 6 );
Perceba que no laço do exemplo acima, o angulo, a cada iteração, é incrementado em 60º (O ângulo da fatia do hexágono que corresponde a ( PI / 3 ) ). Isto é, na primeira iteração, o angulo "a" corrresponde a zero, na segunda, a 60º na terceira a 120º e assim por diante até completar os 360º. Perceba também que, para determinar as coordenadas, foram necessários calculos trigonométricos. Vamos fazer alguns calculos para determinar as coordenadas do hexágono.
int x1 = centroX + ( raio * cos( 0º ) );
int y1 = centroY + ( raio * sin( 0º ) );
int x2 = centroX + ( raio * cos( 60º ) );
int y2 = centroY + ( raio * sin( 60º ) );
int x3 = centroX + ( raio * cos( 120º ) );
int y3 = centroY + ( raio * sin( 120º ) );
.
.
.
int x6 = centroX + ( raio * cos( 300º ) );
int y6 = centroY + ( raio * sin( 300º ) );
Como no exemplo acima o que varia a cada coordenada é apenas o ângulo que é incrementado em 60º, podemos utilizar um for (ou outro loop) para gerar os vetores Xs e Ys do polígono a ser desenhado: o hexágono. Por isso, o código acima foi substituido pelo código abaixo.
int[] vetorX = new int[ 6 ];
int[] vetorY = new int[ 6 ];
for( int i = 0; i < 6; i++ ) {
double a = angulo * i;
vetorX[i] = centroX + (int)Math.round( raio * Math.cos( a ) );
vetorY[i] = centroY + (int)Math.round( raio * Math.sin( a ) );
}
Agora, veja abaixo o código completo:
import java.awt.*;
import javax.swing.*;
public class Hexagono extends JPanel {
public Hexagono() {
super.setPreferredSize( new Dimension( 400, 400 ) );
super.setBackground( Color.BLACK );
}
public void paintComponent( Graphics g ) {
super.paintComponent(g);
int larguraTela = super.getWidth();
int alturaTela = super.getHeight();
int centroX = larguraTela / 2;
int centroY = alturaTela / 2;
int raio = 100;
double angulo = Math.PI / 3.0d;
int[] vetorX = new int[ 6 ];
int[] vetorY = new int[ 6 ];
for( int i = 0; i < 6; i++ ) {
double a = angulo * i;
vetorX[i] = centroX + (int)Math.round( raio * Math.cos( a ) );
vetorY[i] = centroY + (int)Math.round( raio * Math.sin( a ) );
}
g.setColor( Color.WHITE );
g.drawPolygon( vetorX, vetorY, 6 );
}
public static void main(String[] args) {
Hexagono painel = new Hexagono();
JFrame f = new JFrame();
f.setContentPane( painel );
f.setTitle( "Hexágono" );
f.setDefaultCloseOperation( JFrame.EXIT_ON_CLOSE );
f.setSize( 500, 500 );
f.setLocationRelativeTo( f );
f.setVisible( true );
}
}
Veja abaixo o resultado do programa acima:
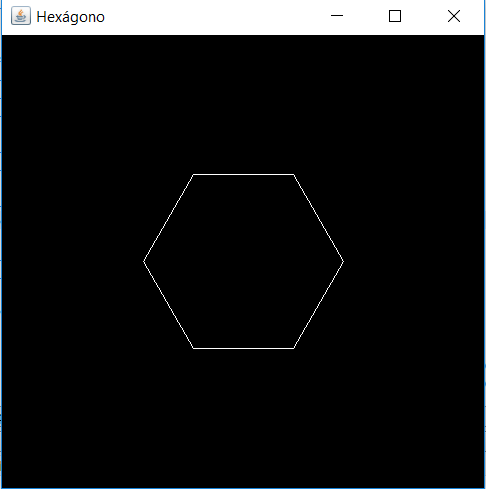
Veja abaixo um programa que fiz que mostra sobre o que é possível fazer com gráficos em puro Java. Trata-se de um jogo produzido em Java com, apenas, a biblioteca gráfica fornecida pela linguagem. Todos os personagens e componentes do jogo são polígonos desenhados em Java. Abaixo o link para download do jogo "Batalha Estrelar":

Para jogar, aperte o espaço para atirar e movimente a nave utilizando as setas do teclado
Download: BE-1.2.jar
E assim termino o primeiro artigo sobre computação gráfica com exemplos em Java. Espero que tenham gostado e, até a próxima!
