Desenho de uma estrela animada
Olá pessoal, este artigo trata de ensinar como desenhar uma estrela em Java 2D.
Caso sinta dificuldade em compreender sobre java swing e Java 2D, bem como, desenhos em Java, recomendo o seguinte artigo para ser estudado antes deste: desenhando-em-java.
Então, vamos lá:
O resultado final deve ficar conforme a figura abaixo:

O painel de desenho tem uma posição na jenala, bem como, largura e altura. Por exemplo, o painel pode ter 500px de largura e 400px de altura. A estrela que queremos desenhar deve ficar centralizada no painel de desenho. Veja abaixo um progótipo da geometria da estrela:
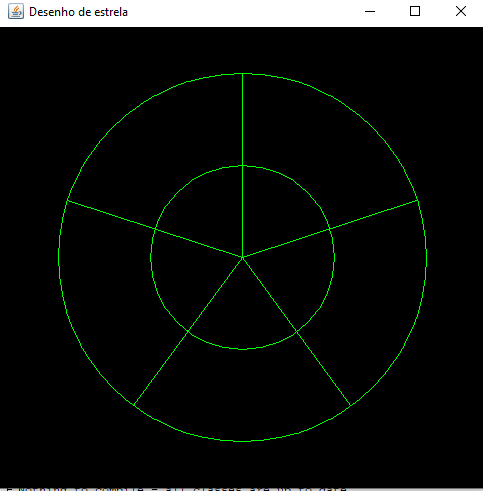
Entenda que há um círculo dentro do outro, com ráio correspondente a metade do ráio do círculo maior. Perceba também que esses 2 circulos foram divididos em 5 partes. Como o ângulo total de um circulo inteiro é 360º, cada fatia do círculo corresponde a 360/5, que é igual a 75º. Logo cada fatia tem 1/5 dos círculos. Mas, você deve estar se perguntando: O que é que isso tem há ver com o desenho de uma estrela?
Então, a estrela tem cinco pontas. Perceba que as linhas que dividem os círculos em 5 fatias poderiam ser as pontas de uma estrela circunscrita no círculo maior. Agora, entenda a figura abaixo:
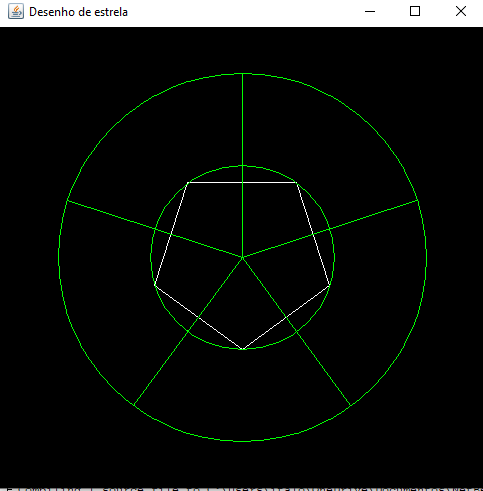
Agora veja abaixo uma figura que ilustra melhor a geometria da estrela:
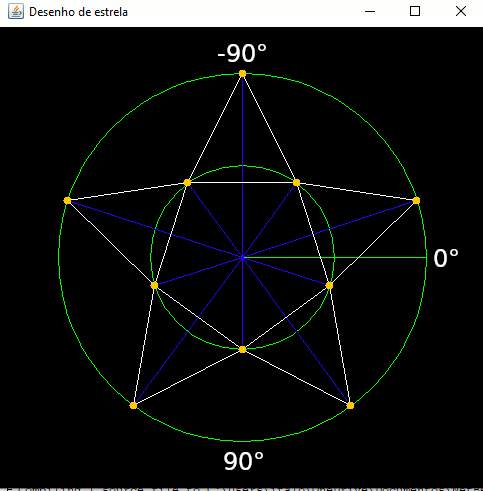
Perceba que a figura acima tem 10 pontos laranjas. São eles que devem ser as 10 coordenadas armazenadas em 2 vetores de 10 posições. Se conseguirmos calcular as coordenadas desses pontos, a sequencia deles corresponde ao polígono representante da estrela que queremos desenhar.
Então veja o código abaixo:
public void paintComponent( Graphics g ) {
super.paintComponent( g );
int w = super.getWidth();
int h = super.getHeight();
int r1 = (int)( RAIO * h );
int r2 = r1/2;
int x = w / 2;
int y = h / 2;
double ainicial = -Math.PI/2;
double ainc = ( 2.0d * Math.PI ) / 5.0d;
int[] xvet = new int[ 10 ];
int[] yvet = new int[ 10 ];
for( int i = 0; i < 5; i++ ) {
double a = ainicial + ( i * ainc );
double a2 = a + ( ainc / 2.0d );
xvet[i*2] = (int)( x + r1 * Math.cos( a ) );
yvet[i*2] = (int)( y + r1 * Math.sin( a ) );
xvet[i*2+1] = (int)( x + r2 * Math.cos( a2 ) );
yvet[i*2+1] = (int)( y + r2 * Math.sin( a2 ) );
}
g.setColor( Color.GREEN );
g.fillPolygon( xvet, yvet, 10 );
g.setColor( Color.BLACK );
g.drawPolygon( xvet, yvet, 10 );
}
Acima, o código fonte da parte lógica relacionada ao desenho da estrela centralizada. Perceba que foram definidos dois vetores de 10 posições para armazenar as coordenadas X e Y dos pontos pintados de laranja na figura anterior. Nas variáveis "w" e "h" ficam armazenadas as dimensões do painel e nas variáveis "x" e "y", ficam as coordenadas do centro do painel de desenho. Perceba que os dois raios: "r1" e "r2", correspondem aos raios dos círculos maior e menor, respectivamente. Perceba o ângulo 0º e o -90º. Queremos que nosso polígono começe com as coordenadas polares (r1, -90º) ou (r1, -PI/2). Perceba também, a variável "ainc", que corresponde a 1/5 do ângulo total do círculo que é 360°. Logo, "ainc" é iqual a 75º, sendo que o valor está em radianos no programa Java acima. Como 180° correspondem a PI, -90º correspondem a -PI/2.
O for tem a variável "i" que varia de "0" a "4". Logo, em cada iteração, as variáveis "a" e "a2" assumem os seguintes valores:
- IT(1) -> i=0, a=-90º , a2=-52,5º
- IT(2) -> i=1, a=-15º, a2=21,5º
- IT(3) -> i=2, a=60º, a2=107,5°
- IT(4) -> i=3, a=135º, a2=172,5º
- IT(5) -> i=4, a=210º, a2=247,5º
A expressão "i*2" corresponde, respectivamente em cada iteração, a: 0, 2, 4, 6, 8
A expressão "i*2+1" corresponde a: 1, 3, 5, 7, 9
Logo, veja agora cada ponto do polígono em coordenadas polares: (r1,-90º),(r2,-52.5º),(r1,-15º),(r2,21.5º),(r1,60º),(r2,107.5°),(r1,135º),(r2,172.5º),(r1,210º),(r2,247.5º)
Para converter de coordenadas polares para cartesianas, basta seguir as seguintes fórmulas:
- X= raio * cos( angulo )
- Y= raio * sen( angulo )
Por isso essas fórmulas foram utilizadas em:
xvet[i*2] = (int)( x + r1 * Math.cos( a ) );
yvet[i*2] = (int)( y + r1 * Math.sin( a ) );
Onde, o raio é "r1", e o ângulo é "a", e os valores "x" e "y" são somados as coordenadas cartesianas para centralizar a estrela. Os valores das coordenadas encontradas com a aplicação das fórmulas é armazenado em "xvet[i*2]", que corresponde a "X" na fórmula, e em "yvet[i*2]", que corresponde a "Y" na fórmula de conversão de coordenadas polares para cartesianas.
A seguir o código completo da classe que desenha a estrela e, também, de uma thread que altera o valor de "ainicial", que inicia em -90º, de modo a rotacionar a figura e, fazendo assim, uma animação com a rotação da estrela:
import java.awt.*;
import javax.swing.*;
public class Estrela extends JPanel implements Runnable {
private final double RAIO = 0.4;
private double ainicial = -Math.PI/2.0d;
public Estrela() {
super.setBackground( Color.WHITE );
}
@Override
public void run() {
while( true ) {
super.repaint();
try {
Thread.sleep( 30 );
} catch ( InterruptedException e ) {
}
ainicial += Math.PI / 96.0d;
}
}
@Override
public void paintComponent( Graphics g ) {
super.paintComponent( g );
int w = super.getWidth();
int h = super.getHeight();
int r1 = (int)( RAIO * h );
int r2 = r1/2;
int x = w / 2;
int y = h / 2;
double ainc = ( 2.0d * Math.PI ) / 5.0d;
int[] xvet = new int[ 10 ];
int[] yvet = new int[ 10 ];
for( int i = 0; i < 5; i++ ) {
double a = ainicial + ( i * ainc );
double a2 = a + ( ainc / 2.0d );
xvet[i*2] = (int)( x + r1 * Math.cos( a ) );
yvet[i*2] = (int)( y + r1 * Math.sin( a ) );
xvet[i*2+1] = (int)( x + r2 * Math.cos( a2 ) );
yvet[i*2+1] = (int)( y + r2 * Math.sin( a2 ) );
}
g.setColor( Color.GREEN );
g.fillPolygon( xvet, yvet, 10 );
g.setColor( Color.BLACK );
g.drawPolygon( xvet, yvet, 10 );
}
public static void main(String[] args) {
Estrela estrela = new Estrela();
JFrame f = new JFrame();
f.setTitle( "Desenho de estrela" );
f.setContentPane( estrela );
f.setDefaultCloseOperation( JFrame.EXIT_ON_CLOSE );
f.setSize( 500, 500 );
f.setLocationRelativeTo( f );
SwingUtilities.invokeLater( () -> {
f.setVisible( true );
Thread t = new Thread( estrela );
t.start();
} );
}
}
Experimente colocar o código acima numa classe Java, compilar e rodar para ver o resultado!
É isso pessoal, até a próxima!
