Backtracking
O backtracking é um algoritmo que funciona de forma parecida com algoritmos de força bruta. No entanto, o backtracking oferece um meio de eliminar muitas das possibilidades, funcionando como força bruta apenas se o busca não tiver solução.
Um exemplo de problema que pode ser resolvido de modo otimizado com o backtracking é o problema imprimir todas as permutações de três zeros ou uns que têm apenas um único zero. Veja a árvore de possibilidades abaixo:
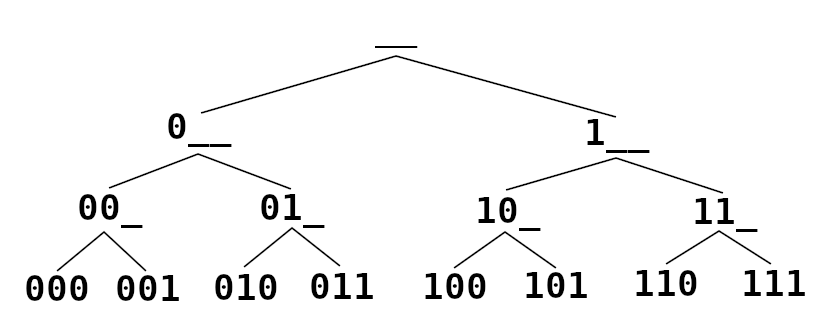
Perceba que não é necessário verificar todas as possibilidades para imprimir as combinações que contêm apenas um único zero. Veja as eliminações na árvore abaixo:
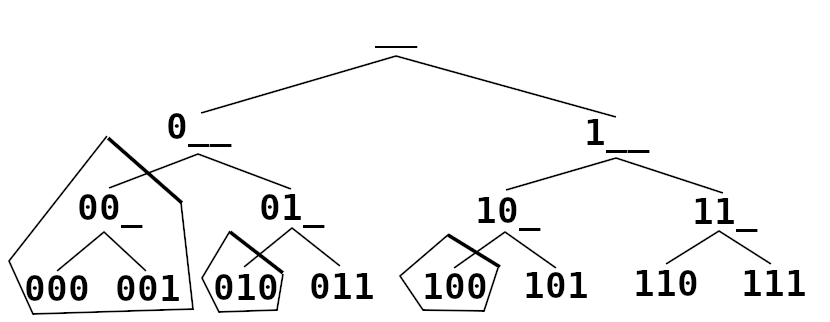
Na árvore de possibilidades acima, as soluções circuladas são descartadas.
Para entender melhor a aplicação do backtracking para o problema de permutações de zeros e uns, pense num algoritmo que, a cada iteração de um laço, uma nova combinação de três zeros ou uns é gerada. Claro, o algorimo gera de um em um números. Então, quando, a combinação atual já tem dois zeros, não há necessidade de continuar até gerar as possibilidades de combinações que iniciam com dois zeros. Pois, tais combinações certamente terão mais que um zero.
Função objetivo
No exemplo das combinações de zeros e uns, se pode eliminar algumas possibilidades. Isto é, o algoritmo que resolve o problema utiliza um mecanismo para verificar se é necessário continuar derivando a árvore a partir do nó atual.
Em outras palavras, a verificação que evita que todas as possibilidades sejam verificadas é feita através de uma Função Objetivo.
Oito rainhas
Um outro problema famoso que pode ser resolvido com a técnica backtracking é o problema das oito rainhas. Isto é, dado um tabuleiro de xadrez convencional: 8x8, colocar oito rainhas em celulas do tabuleiro de modo que nenhuma rainha esteja ao alcance de outra, respeitando-se as regras de movimentos da rainha em um jogo de xadrez. Veja a solução abaixo:
backtracking( rainhas, i )if ( i > 7 )return trueok = falsej = 0;while ( ok == false ) and ( j < 8 ) dorainhas[ i ] = j;if ( verificaCaptura( rainhas, i ) = false )ok = backtracking( rainhas, i+1 )j++return ok
Perceba o seguinte: O vetor rainhas é unidimensional. Ele tem tamanho 8, onde, cada posição dele armazena a posição x (na horizontal) da rainha. Isto é, o índice do vetor corresponde ao y e o elemento da posição y, corresponde ao x da rainha.
Agora perceba que há uma chamada recursiva na linha 10, logo, é necessária uma condição de parada pra evitar o loop infinito. Isto é, a condição de parada é 'i>7'. Já que o tabuleiro de xadrez é 8x8.
Se i <= 7, então o algoritmo pode derivar as possibilidades de posições da rainha na linha atual de índice 'i'. Isto é, atribui ao vetor de rainhas na posição 'i' o valor 'j' e, então, verifica através da função objetivo: verificaCaptura, se na configuração atual de rainhas, alguma rainha captura a outra. Se há captura, não há necessidade de derivar esse início de solução. Se não há captura, então este é um início de solução candidata e, então, esta solução deve ser derivada com a chamada recursiva para busca pela posição da rainha na linha seguinte, isto é, a linha 'i+1'.
Perceba que o retorno da chamada recursiva funciona como condição de parada do loop while que, caso uma solução válida seja encontrada, então o loop para imediatamente sem necessitar verificar as posições restantes da linha no tabuleiro.
Agora, veja abaixo a solução encontrada pelo algoritmo backtracking aplicado ao problema das oito rainhas:

Na solução acima, o 'R' corresponde à uma rainha e o '*', à uma célula vazia.
Atenção: a implementação da função verificaCaptura está no programa disponibilizado para download no final deste artigo.
Finalizando
Como recurso auxiliar para o aprendizado do backtracking aplicado ao problema das oito rainhas, eu preparei um programinha escrito em linguagem C que implementa o algoritmo. Faça o download logo abaixo:
Link: oito_rainhas.c
O CodeBlocks foi utilizado como IDE para desenvolvimento do programa acima.
E, é isso pessoal, até a próxima!
Inspirado em
Cormen. H. Thomas et. al, 2002 - Algoritmos teoria e prática - 2 ed. Rio de Janeiro - RJ, Brasil, 2002
