Caminho Mínimo
O algoritmo do caminho minimo tem muitas aplicações. É comum de ser utilizado quando se deseja, por exemplo, dado um conjunto de cidades e as distâncias entre elas, determinar o caminho de menor custo (menor distância total) entre uma cidade e outra. Entre as cidades de origem e de destino, podem haver muitas cidades e muitos diferentes caminhos.
Para aplicar um algoritmo que determine o caminho minimo entre uma origem e um destino, é necessária a representação do pontos (que podem ser cidades) e suas distâncias em um grafo não orientado. Para esse artigo, o grafo de cidades deve ser representado em uma matriz de adjacências.
Matríz de adjacências
Para um exemplo, vamos considerar 9 cidades representadas pelas letras de A até I. Onde o A corresponde ao índice 0, o B corresponde ao índice 1, e assim sucessivamente. As distâncias estão representadas na matriz de adjacências e indexadas pelos índices começando do zero conforme abaixo:

Você pode notar na matriz acima que o elemento da posição (0,1), que corresponde a (A,B), indica que a distância da cidade A até a cidade B corresponde a esse elemento: o 4. Note também que a distância de A até B é igual a distância de B até A. Logo, (0,1) tem o mesmo valor que (1,0). A distância de cada cidade para ela mesma é 0 e quando não há caminho direto entre duas cidades, a distância também fica, nesse exemplo, com valor zero também.
Veja abaixo outra representação das distâncias entre as cidades:
(A,B) = (B,A) = 4
(B,C) = (C,B) = 8
(C,D) = (D,C) = 7
(D,E) = (E,D) = 9
(E,F) = (F,E) = 10
(F,G) = (G,F) = 2
(G,H) = (H,G) = 1
(H,I) = (I,H) = 7
(G,I) = (I,G) = 6
(C,I) = (I,C) = 2
(C,F) = (F,C) = 4
(D,F) = (F,D) = 14
(C,H) = (H,C) = 11
O algoritmo de dijkstra
Primeiramente vamos a ideia do algoritmo de dijkstra para o encontro do caminho mínimo.
A ideia básica do algoritmo é percorrer todos os nos do grafo (cada nó uma cidade entre A e I) e, calcular a distância minima encontrada até então para o nó atual. Por exemplo, a distância de A até I percorrendo as cidades: A, B, C, D, E, F, G, H, I correspondem a soma dessas distâncias que é: 4+8+7+9+10+2+1+7=48. No entanto, se com mais algumas iterações do algoritmo, o nó I for encontrado novamente, sendo que pelo caminho: A, B, C, I, então a soma é: 4+8+2=14. Logo, a distância menor encontrada até então de A até I passa a ser 14, e não mais, 48.
O pseudocodigo
caminho_otimo( MADJ, n, r, DISTS, SOLUCAO )for i=0 to n-1 doDISTS[ i ] = INFINITYSOLUCAO[ i ] = -1Q[ i ] = i;DISTANCIAS[ r ] = 0qlen = nwhile( qlen > 0 )u = extract_min( Q, DISTS, &qlen )for v=0 to n-1 doif ( MADJ[ u ][ v ] != 0 )if ( DISTS[ u ] + MADJ[ u ][ v ] < DISTS[ v ] )DISTS[ v ] = DISTS[ u ] + MADJ[ u ][ v ]SOLUCAO[ v ] = u
O algoritmo do caminho de custo mínimo recebe 5 argumentos. O primeiro é a matriz de adjacências, o segundo 'n' é o número de nós (cidades), o terceiro 'r' é o índice da cidade de origem, o quarto é um vetor de distâncias que é alterado pelo algoritmo com as distâncias entre a cidade de origem e todas as outras, e, por último, o quinto parâmetro é o vetor onde será armazenada a solução. Isto é, o caminho ótimo encontrado pelo algoritmo.
Primeiramente o algoritmo deve inicializar os vetores de distâncias e solução e um novo vetor onde ficam armazenados inicialmente, todos os índices de cada nó (cidade) na matriz de adjacências.
Após isto, é armazenado zero como a distância do nó de origem até ele mesmo e a variável 'qlen' é o número de elementos no vetor 'Q' que, inicialmente, corresponde ao número de cidades (dimensão da matriz de adjacências).
No loop while da linha 10, a condição de parada é não haver mais algum índice de alguma cidade no vetor 'Q'. Na linha 11, é procurado o índice da cidade presente em 'Q' com a menor distância da origem encontrada até então. Após encontrado o nó de menor distância da origem, ele é removido do vetor 'Q' até não haver mais nenhum elemento em 'Q' e o loop finalizar.
Na linha 11, tem o for que tem como objetivo percorrer a linha na matriz de adjacências do índice retornado pela função 'extract_min'. Isto é, são descartadas (na linha 12) as cidades com distância igual a zero.
Nas linhas 13, 14 e 15 está a lógica principal do algoritmo. Isto é, dado o elemento 'u' e um elemento 'v' vizinho de 'u', verificar se a menor distância encontrada da origem até 'u', mais a distância de 'u' até 'v' é menor que a distância da origem até 'v', se sim, na posição do vetor 'DISTS' correspondente a cidade 'v' é armazenada a nova menor distância encontrada. E, no vetor 'SOLUCAO', é armazenada uma referência a cidade 'u'. Isto é, depois de 'v', o próximo elemento da solução deve ser 'u'.
Os vetores DISTS e SOLUCAO
Veja e analise abaixo o resultado de uma implementação do algoritmo de dijkstra para o cálculo do caminho ótimo do exemplo deste artigo:
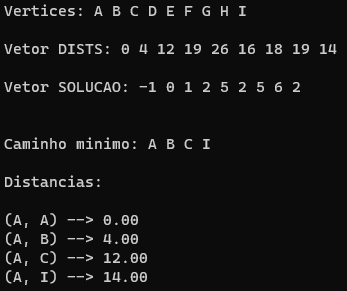
Perceba que foi escolhida como cidade de origem a cidade A e como cidade de destino a cidade I. Por exemplo: na posição 0 do vetor está o valor 0. Isso porque o índice 0 corresponde a cidade A e a menor distância da origem A até A é zero. A menor distância de A até a cidade G é 18, porque o índice 6 corresponde a cidade G e na posição 6 está armazenado o valor 18. Do mesmo modo, a menor distância de A até I é 14.
O vetor solução armazena uma lista encadeada invertida. Isto é, o último elemento tem uma referência para o penúltimo, o penúltimo tem referência para o antepenúltimo, e assim, o segundo tem uma referência para o primeiro. Veja a lógica abaixo:
Para determinar as cidades de I até A, basta fazer conforme o seguinte:
SOLUCAO = -1 0 1 2 5 2 5 6 2
8 = I,
SOLUCAO[ 8 ] = 2 = C,
SOLUCAO[ 2 ] = 1 = B,
SOLUCAO[ 1 ] = 0 = A,
SOLUCAO[ 0 ] = -1 = equivalente a NULL.
Logo, as cidades de A até I são: A, B, C, I
A cidade I é a primeira e tem índice 8 (n-1), logo, a próxima cidade é a cidade de índice 2, a cidade C. Na cidade 2 tem uma referência à cidade 1 que é a cidade B e na posição 1 tem uma referência à cidade 0, a cidade A, na posição 0 está o valor -1. Ou seja, depois de A, não há nenhuma outra cidade. Até porque, A já é a cidade de origem.
A função extract_min
Veja abaixo uma implementação em linguagem C da função extract_min:
int extract_min( int* Q, int* dists, int* tam ) {int i, q;int menor = INFINITY;int k = -1;for( i = 0; i < *tam; i++ ) {if ( dists[ Q[i] ] < menor ) {menor = dists[ Q[i] ];k = i;}}q = Q[ k ];for( i = k; i < (*tam)-1; i++ )Q[ i ] = Q[ i + 1 ];*tam = (*tam) - 1;return q;}
A função extract_min apenas remove o elemento de menor distância de Q e o retorna. Decrementando também tamanho de Q.
Uma variação do algoritmo: O A*
Uma variante do algoritmo do caminho mínimo é conhecida como A* - A estrela. Esse algoritmo tem aplicações quando se tem uma origem e destino e obstaculos. O problema é, dados os obstáculos, qual o caminho mínimo da origem ao destino. Ou, ainda, qual a direção de movimento que, após efetuado o movimento, a origem passa a estar ainda mais próxima do destino.
Há outro artigo disponível neste site sobre uma aplicação do A* que foi aplicado em um jogo de pacman. Onde, os personagens inimigos precisam determinar qual o caminho mínimo até o pacman no tabuleiro do jogo. Acesse a página do jogo e faça o download dele para testá-lo clicando aqui.
Finalizando...
Como recurso auxiliar para o aprendizado do algoritmo do caminho mínimo, eu preparei um programinha escrito em linguagem C que implementa o algoritmo. Faça o download logo abaixo:
Link: caminho_minimo.c
O CodeBlocks foi utilizado como IDE para desenvolvimento do programa acima.
E, é isso pessoal, até a próxima!
Inspirado em
Cormen. H. Thomas et. al, 2002 - Algoritmos teoria e prática - 2 ed. Rio de Janeiro - RJ, Brasil, 2002
