Merge Sort - Ordenação por intercalação

O mergesort é um algoritmo de ordenação por intercalação que utiliza a técnica de divisão e conquista, um método recursivo de ordenação onde se busca dividir o problema principal em subproblemas semelhantes de modo que esses subproblemas são resolvidos recursivamente para, então, ser resolvido o problema principal. Veja a seguir uma ilustração de como funciona a divisão, conquista e intercalação no mergesort:

Abaixo, a arvore que ilustra a divisão do arranjo principal em subarranjos recursivamente de cima para baixo na árvore:

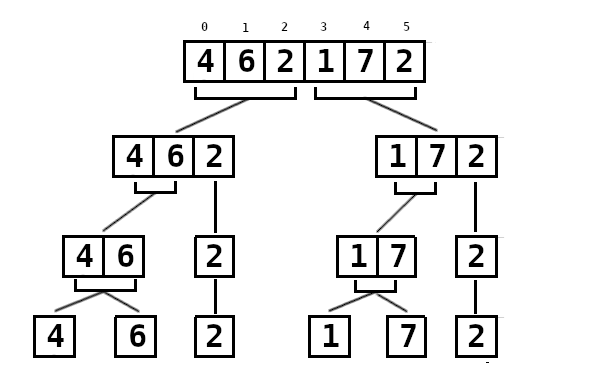
Abaixo, a arvore que ilustra a conquista e intercalação ordenada dos arranjos menores até cada arranjo, um nível acima na arvore, estar completamente ordenado.

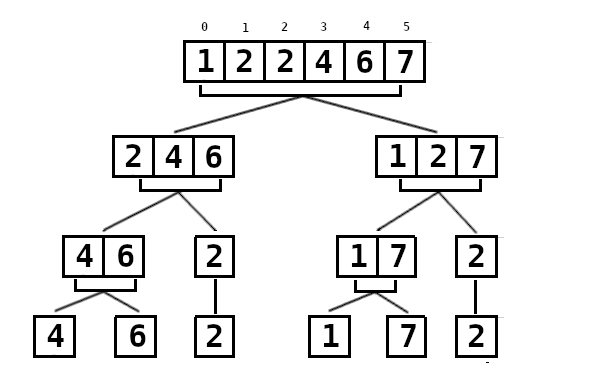
A intercalação

Para o mergesort funcionar bem, é necessária uma solução eficiente de intercalação (Ou merge). Veja abaixo um exemplo de intercalação e, mais uma vez, analise de baixo para cima:

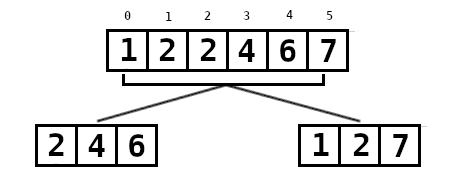
Perceba que os dois vetores de 3 elementos ordenados são intercalados de modo a formar o vetor principal com os 6 elementos ordenados. Para melhor compreensão do processo de intercalação, vamos à um exemplo:

Imagine os 2 seguintes arranjos:

    A=[3, 6, 9]
    B=[1, 3, 7]

O objetivo é intercalá-los para compor o vetor principal C.

Primeiramente, podemos entender que o vetor C resultante terá o número de elementos de A somado ao número de elementos de B. Então vamos lá!

O vetor C deve corresponder ao arranjo C abaixo:

    A=[3, 6, 9]
    B=[1, 3, 7]
    C=[1, 3, 3, 6, 7, 9]

A lógica é a seguinte: Compara-se A[0] com B[0]. Como B[0] é menor, o C[0]=B[0]. Em seguida, o número de B a ser comparado passa a ser o próximo, dado que o primeiro já foi colocado em C. Então, compara-se A[0] com B[1]. Como são iguais, se pode pegar o primeiro: A[0] para ser colocado em C. Logo, C[1]=A[0] e o próximo elemento de A a ser comparado é o A[1]. Feito isso, compara-se A[1] com B[1]. B[1] é menor e, portanto, este é que é colocado em C. Logo, C[2]=B[1]. Então, compara-se A[1] com B[2]. A[1] é menor. Logo, C[3]=A[1]. Então, compara-se A[2] com B[2] e, então, C[4]=B[2]. Como agora todos os números do vetor B já foram inseridos em C, se pode inserir o restante dos números em A. No caso, resta apenas A[2]. Logo, C[5]=A[2].

Veja outro jeito de entender a intercalação em C:

    C[0]=B[0]
    C[1]=A[0]
    C[2]=B[1]
    C[3]=A[1]
    C[4]=B[2]
    C[5]=A[2]

E se o arranjo fosse como abaixo:

    A=[1, 8, 9]
    B=[8, 9, 10]

Então a intercalação acontece conforme abaixo:

    C[0]=A[0]
    C[1]=A[1]
    C[2]=B[0]
    C[3]=A[2]
    C[4]=B[1]
    C[5]=B[2]  

Logo, o vetor intercalado C é:

    C=[1, 8, 8, 9, 9, 10]

O pseudocódigo do merge

 merge( C, p, q, r )     
   n1=q-p+1              
   n2=r-q                
   A=[]                  
   B=[]                  
   for k = 0 to n1-1 do  
     A[k] = C[p+k]       
   for k = 0 to n2-1 do  
     B[k] = C[q+1+k]     
   A[n1]=∞         
   B[n2]=∞         
   i=0                   
   j=0                   
   for k = p to r do     
     if ( A[i] <= B[j] ) 
       C[k] = A[i]       
       i++               
     else                
       C[k]=B[j]         
       j++               

O algoritmo recebe o vetor C de modo que C[p..q] corresponde ao vetor A na explicação anterior e C[q+1..r] corresponde ao vetor B. Ambos A e B ordenados. Então, pelo algoritmo representado acima, primeiro, calcula-se a quantidade de elementos de C que correspondem ao vetor A e a quantidade de elementos de C que correspondem ao vetor B. Feito isso, entre as linhas 6 e 9, os valores C[p..q] são colocados em A e os valores C[q+1, r] são colocados em B.

Nas linhas 10 e 11, perceba que é acrescentado, tanto em A, quanto em B, mais um elemento com valor ∞. Assim, o tamanho do vetor A, passa a ser n1+1 e o tamanho do vetor B, passa a ser n2+1.

A partir da linha 14 está o conteúdo do for que realiza a intercalação. Ou seja, dado que n1+n2 é igual a r-p+1, se pode garantir que, a cada iteração, o valor de C[k] recebe um dos elementos de A[0..n1-1] ou um dos elementos de B[0..n2-1].

Outro detalhe importante é a utilidade de se colocar valores infinitos ao final dos vetores A e B. Isto é, se por exemplo, todos os valores de A, com exceção de ∞ forem inseridos em C, o restante dos elementos de B, com exceção de ∞ são menores que ∞. Logo, o restante dos elementos de B, B[0,n2-1], são inseridos. Isso porque, ao comparar os elementos de B restantes com o elemento ∞ de A, os elementos de B são menores e, assim, são todos colocados ao final do vetor C, com exceção do valor ∞

Como o algoritmo não tem sequer laços aninhados, e o terceiro for tem maior custo computacional de tempo que os outros. Logo, é facil perceber que a ordem de crescimento corresponde a θ(n)=n, onde n = r-p+1.

Pseudocódigo do mergesort

  mergesort( A, p, r )         
    if ( p < r )               
      q = p + (( r-p )/2);     
      mergesort( A, p, q );    
      mergesort( A, q+1, r );  
      merge( A, p, q , r );    

Agora suponha A o arranjo de números a serem ordenados e o número de elementos em A armazenado na variável 'n'. Então o mergesort deve ser chamado como a seguir:

  mergesort( A, 0, n-1 )  

Em pascal, por exemplo, caso o vetor A tenha seus índices definidos entre [1..n] então a chamada ficaria como a seguir:

  mergesort( A, 1, n )  

Explicação do algoritmo

Dado o algoritmo de ordenação representado em pseudocódigo, se pode facilmente perceber que a função mergesort faz internamente duas chamadas recursivas a ela mesmo.

Não é complicado entender a ideia básica do mergesort. As duas chamadas recursivas são porque o problema maior é resolvido dividindo-se ele em dois problemas menores e esses dois problemas menores podem ainda serem divididos cada um em mais dois problemas menores, conforme uma arvore que pode ilustrar essas chamadas recursivas já listada anteriormente.

Então, primeiro é calculado o valor mediano chamado de 'q' que está no meio entre 'p' e 'r'. Aqui fica evidenciada a idéia de difidir o arranjo A em dois de tamanho iguais (ou o primeiro com, no máximo, um elemento a mais que o segundo). Logo, se o vetor A tiver 6 elementos: primeiro, ordena-se os três primeiros elementos (primeira chamada recursiva), e depois, os três últimos (segunda chamada recursiva) para, então, intercalar (função merge) os dois subarranjos e formar o vetor A ordenado.

O número 'q' corresponde ao índice que divide esse arranjo nas suas duas partes menores, e o IF, é a condição de parada. Uma condição de parada é necessária a toda solução recursiva para evitar loop infinito e a parada do mergesort é quando o p e r são iguais. Isto é, indices do mesmo elemento do Arranjo A.

O cálculo da complexidade do algoritmo

Para analizar a complexidade da função mergesort, podemos escrever uma recorrência em função de 'n' como a seguir:

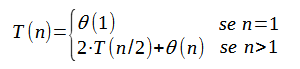
Conforme a imagem acima, se pode considerar que: se 'n'=1, isto é houver apenas um elemento para ser ordenado, a verificação da condição do if que pode ter uma ordem de crescimento θ(1) e é executada uma vez, e considerada falsa e o bloco de código do IF não é executado.

Se 'n'>1, então o vetor é dividido em 2 de tamanho aproximado à n/2 cada. Logo, são duas cmamadas recursivas à T(n/2) somada a operação de merge que tem ordem de crescimento igual a θ(n).

Se considerarmos que θ(1) corresponde a um valor constante qualquer e θ(n) é igual a 'n' vezes esse valor qualquer, então, caso esse valor qualquer seja representado por uma constante 'c', a recorrência pode ser expressa como a seguir:

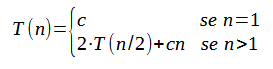
Para facilitar a compreensão, vamos pegar um exemplo de vetor a ser ordenado cuja árvore que representa as chamadas recursivas do mergesort tem profundidade 4. Isto é, 'n' (tamanho do vetor) igual a 8. Então, analise a figura abaixo:

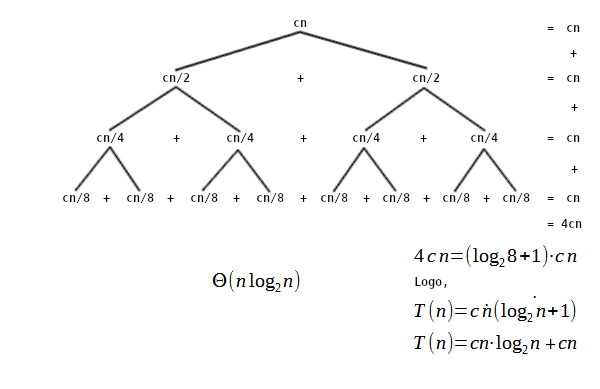
Pela figura acima, se pode notar que o vetor de 8 elementos é dividido em 2 de tamanho 4 = 8/2, logo após, cada um dos vetores de tamanho 4, são divididos 2 vetores de tamanho 2 = 4/2 e cada vetor de tamanho 2 é dividido em 2 vetores de tamanho 1 = 2/2. A constante c corresponde ao tempo de execução de uma instrução qualquer com ordem de crescimento θ(1) e ela multiplica o novo número de elementos de cada vetor.

Somando todos os valores da árvore, se consegue obter o valor 4cn. Logo, 4 corresponde a altura da árvore e se utilizarmos esse valor em função da altura, ele pode ser substituído por 'log 8 + 1' (logarítmo na base 2). O 8 corresponde ao número de elementos, logo, o tempo em função de n fica como a seguir:

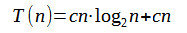
Como c é constante e 'cn*log(n)' tem ordem maior que 'cn', então a ordem de crescimento do algoritmo pode ser expressa como abaixo:

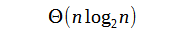
Conclusão

Esse foi o artigo escrito sobre o mergesort, um algoritmo de intercalação mais rápido se comparado com algoritmos de ordenação de ordem θ(n²) e que utiliza a técnica de divisão e conquista para ordenar um Arranjo de elementos. No entanto, há uma limitação de memória, dado que, é necessário mais dois vetores auxiliares de tamanho (n/2 + 2), onde n é o tamanho do arranjo de elementos principal.

Como recurso auxiliar do aprendizado do algoritmo mergesort, eu preparei um programinha escrito em linguagem C que implementa o algoritmo e mostra o resultado do vetor ordenado. Faça o download logo abaixo:

Link: mergesort.c

O CodeBlocks foi utilizado como IDE para desenvolvimento do programa ordenação acima.

E, é isso pessoal, até a próxima!

Inspirado em

Cormen. H. Thomas et. al, 2002 - Algoritmos teoria e prática - 2 ed. Rio de Janeiro - RJ, Brasil, 2002