Iluminação de formas em 3D
Quando utilizamos um software que desenha formas 3D na tela de um computador, televisão ou outro dispositivo de saída, geralmente, percebemos que as formas que podem ser, por exemplo, personagens de um jogo eletrônico, são pintadas na tela de acordo com uma ou mais cores. Isto é, não são apenas desenhadas, mas, coloridas. No artigo anterior, escrevi sobre como desenhar uma forma geométrica básica em 3D sem o uso de qualquer framework. Ou seja, foi abordado um meio de desenhar formas tridimensionais sem o uso de bibliotecas gráficas como: OpenGL ou Java3D, utilizando-se, apenas, das funções de desenho e pintura em 2D para o desenho das formas representadas no espaço tridimensional. No entanto, no artigo anterior, não mostrei uma forma de colorir as formas geométricas. Isso será mostrado aqui, logo a seguir!
Atenção: Esse artigo é a continuação do artigo sobre introdução a computação em 3D.
Para visitar a página de introdução, clique aqui.
Primeiramente, precisamos entender como que pessoas podem enxergar objetos no mundo real de acordo com a incidência de luz sobre tal objeto e a composição química dele. Isto é, para enxergar-mos um objeto no mundo real, precisamos que uma fonte de luz esteja acesa, caso contrário, enchergamos apenas o preto, pois, estamos no escuro.
Para enxergarmos algo, é necessária uma fonte de luz ativa que emita luz em todas as direções provenientes dela. Inclusive, é muito importante aqui, entender que os raios de luz se propagam em linha reta.
Então, o computador também pode utilizar uma abordagem parecida com a do mundo real. Por exemplo, o desenho de um objeto colorido no universo virtual, que é o espaço de desenho tridimensional, depende de uma, ou várias, fontes de luz. Onde, cada fonte de luz tem uma coordenada e propaga luz em todas as suas direções. Então, os raios de luz (propagados em linha reta), atingem as faces dos objetos e, assim, o observador, que observa através da tela do computador, pode enxergar os objetos com as suas devidas cores. É importante notar que cada face do objeto pode ter a cor escurecida ou esclarecida, dependendo do ângulo de incidência da luz. Veja a imagem abaixo:
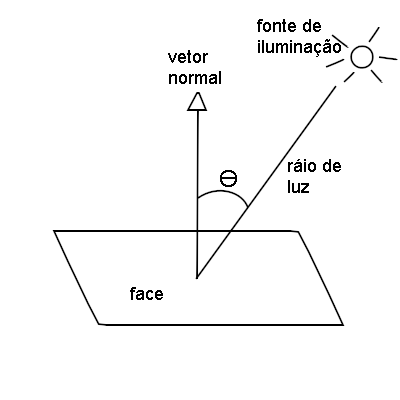
Analisando a imagem acima, você pode perceber: a face, a fonte de luz, o vetor normal perpendicular a face, o raio de luz e o ângulo Ɵ entre o vetor normal e o vetor que corresponde ao raio de luz.
O vetor normal
O vetor normal é perpendicular a um plano, em que, para o cálculo dele, são necessários dois vetores (não colineares) pertencentes ao plano. No entanto, é necessário considerar também que, para cada plano, podem existir dois vetores normais, um apontando a partir de um lado do plano e outro apontando a partir do outro lado do plano. Veja a imagem abaixo:
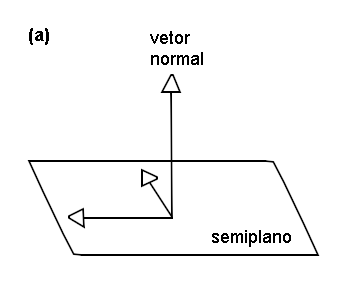
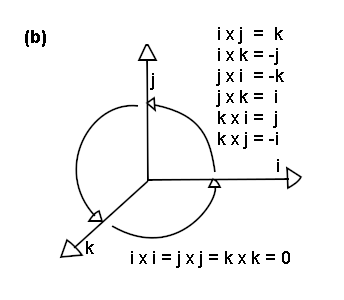
Em (a), se pode perceber o vetor normal perpendicular a dois vetores pertencentes ao mesmo plano da face. Em (b), se pode perceber que o produto vetorial entre os vetores (i,j e k), é positivo, se a direção é no sentido anti-horário, e negativo, caso contrário. Você pode se basear nas setas. Por exemplo, i x j = k, mas j x i = -k !
É necessário entender pela figura (a) que o vetor normal é o produto vetorial dos dois vetores pertencentes a face. Então, vamos calcular o produto vetorial entre dois vetores u e v, logo abaixo:
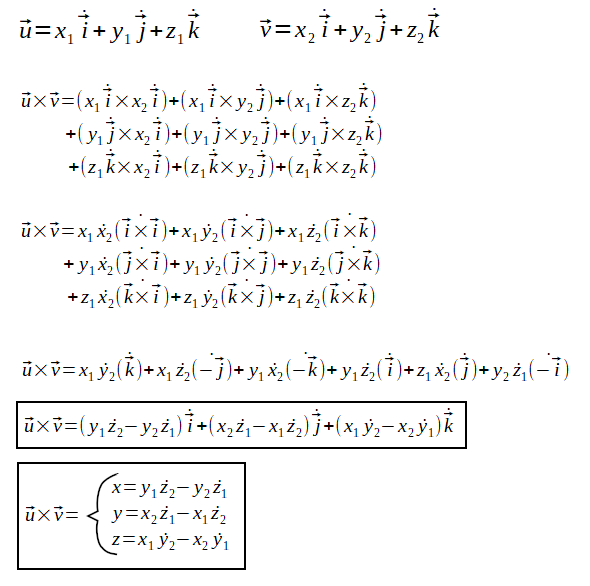
Como resultado dos cálculos acima, se pode perceber os valores para x, y, z do vetor normal que é perpendicular aos vetores u e v. Veja na figura anterior que o vetor normal é perpendicular aos vetores pertencentes a face, isto é, os vetores pertencentes a face podem ser, nos cálculos acima, referenciados por u e v. No entanto, cada face pertence a um plano e, cada plano, pode ter dois vetores perpendiculares a ele (um oposto ao outro). Então, é necessário calcular o vetor normal na direção certa para que o lado correto da face seja pintado. Veja a figura abaixo:
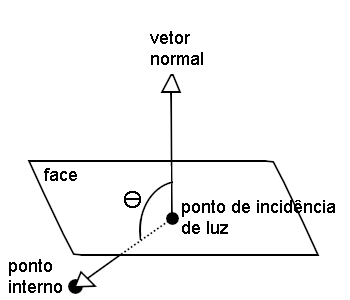
Perceba na figura acima que há um ponto interno cujo vetor é relativo ao ponto de incidência de luz. Esse vetor aponta para o ponto interno que deve ser um ponto interno ao objeto geométrico que se deseje pintar. Assim, entre os dois diferentes vetores normais perpendiculares ao plano da face, escolhe-se o vetor cujo ângulo entre ele e o vetor do ponto interno é maior que 90º. Isso significa que, se o ângulo obtido com o vetor encontrado for menor que 90º, deve-se multiplicá-lo pelo escalar -1. É importante esclarecer que, para essa técnica funcionar para qualquer objeto, é necessário que os mesmos sejam convexos.
O vetor e ângulo de incidência de luz
Outro elemento importante do cálculo da cor sob a qual uma face de um objeto deve ser pintada, conforme a incidência de luz nela, é o vetor relativo ao ponto de incidência de luz e que aponta para o ponto de luz. Esse vetor será referenciado aqui como o vetor de incidência de luz. Para calculá-lo, basta subtrair do ponto de luz, o ponto de incidência de luz na face. Veja a ilustração do ângulo formado entre o vetor normal e o vetor de incidência de luz:
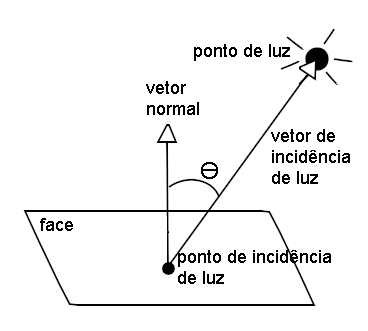
A figura acima ilustra o ângulo de incidência de luz Ɵ que deve ser calculado sob os dois vetores: vetor normal e vetor de incidência de luz.
Para o cálculo do ângulo de incidência de luz, deve-se proceder com uso da seguinte fórmula:
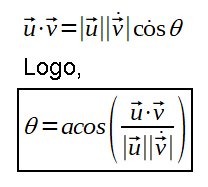
Na fórmula acima, o acos é o arco cosseno e, através dela, se pode calcular o ângulo Ɵ entre dois vetores quaisquer, referenciados na fórmula por: u e v. Então, podemos aplicar a fórmula acima para o cálculo do ângulo de incidência de luz. Isto é, o vetor u podemos associar, por exemplo, ao vetor normal e, o vetor v podemos associar ao vetor de incidência de luz.
A porção de cor da face
Uma vez calculado o ângulo de incidência de luz, se pode calcular a porção de cor que deve ser aplicada a face. Isto é, quanto menor o ângulo Ɵ, maior a intensidade de luz. Logo, maior a porção de cor sob a qual a face deve ser pintada. Quanto maior o ângulo, menor a intensidade de luz e mais escura a cor da face. É importante destacar que o ângulo de incidência Ɵ varia de 0º a 90º, já que, se o ângulo for maior que 90º, o raio de luz não atinge a face.
Veja abaixo o cálculo do fator da porção de cor que é o somatório dos fatores de cada fonte de luz cujo ângulo de incidência calculado é menor que 90º (ou π/2 em radianos):
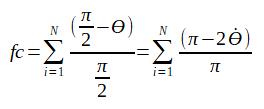
Na fórmula acima, o N corresponde a quantidade de fontes de luz cuja luz ilumina a face, isto é, cujo ângulo de incidência é menor que 90º. Perceba que os ângulos da fórmula estão em radianos.
Uma vez calculado o somatório dos fatores de porção de cor, se pode multiplicá-lo pelos componentes da cor RGB, e, assim, encontrar a porção de cor da face. Claro, se você estiver utilizando outro sistema de representação de cores diferente do RGB, deve proceder de modo análogo. Então, veja abaixo o cálculo da porção de cor no sistema RGB:
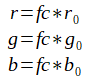
Caso um dos componentes de cor RGB encontrados com o cálculo acima seja maior que 255 (Máxima porção de cor - a porção de cor varia de 0 a 255 em Java), deve-se setar o valor do componente como 255. Por exemplo, se o r for maior que 255, ele deve ser alterado para valer 255. Perceba que a variação de 0 a 255 é proporcional a 0% e 100%. Por exemplo: 256 de r, 128 de g e 64 de b, correspondem, respectivamente, a 100% de r, 50% de g e 25% de b. Entenda também que as porções de cor variam de 0 a 255, não de 1 a 256, por isso, 256 de cor corresponde ao fator: 255 = 256-1.
Faces de objetos 3D
As faces de uma figura geométrica tridimensional são compostas por conjuntos de vértices que formam polígonos. Esses polígonos podem ter as coordenadas de seus pontos determinadas após a projeção em 2D dos vértices do objeto. Então, veja abaixo os vértices e faces de um cubo de lado L:
l = L/2;
V1( -l, -l, -l );
V2( -l, l, -l );
V3( l, l, -l );
V4( l, -l, -l );
V5( -l, -l, l );
V6( -l, l, l );
V7( l, l, l );
V8( l, -l, l );
F1( V1, V2, V3, V4 );
F2( V5, V6, V7, V8 );
F3( V1, V2, V6, V5 );
F4( V2, V3, V7, V6 );
F5( V3, V4, V8, V7 );
F6( V4, V1, V5, V8 );
Faces visíveis
Outro cálculo importante para o desenho e pintura de formas geométricas em 3D é o que determina se uma face é visível ou não. Isto é, quando um objeto está sendo visualizado, as faces de traz não são visíveis. Mas, como determinar se a face deve ser visível? É simples! Basta calcular o vetor normal da face e verificar a coordenada Z dele. se o valor de Z for maior que zero, a face deve ser visível, caso contrário, ela não deve ser visível. Entenda qua quando o objeto é rotacionado, suas faces visíveis pode mudar! Inclusive, o cálculo para determinar se uma face é visível, deve ser feito após a aplicação das transformações geométricas e projeção em perspectiva.
O programa
Desenvolvi um programa exemplo que desenha um cubo e o pinta conforme a teoria apresentada aqui e permite a visualização em diversos ângulos através do arrastar e soltar do mouse. Baixe-o, execute-o e estude-o!
Foi adicionada uma nova classe que chamei de "MatUtil". É nessa classe onde ficam os métodos com implementações dos cálculos apresentados aqui. Dê uma olhada nela!
Abaixo uma captura de tela do programa em execução:
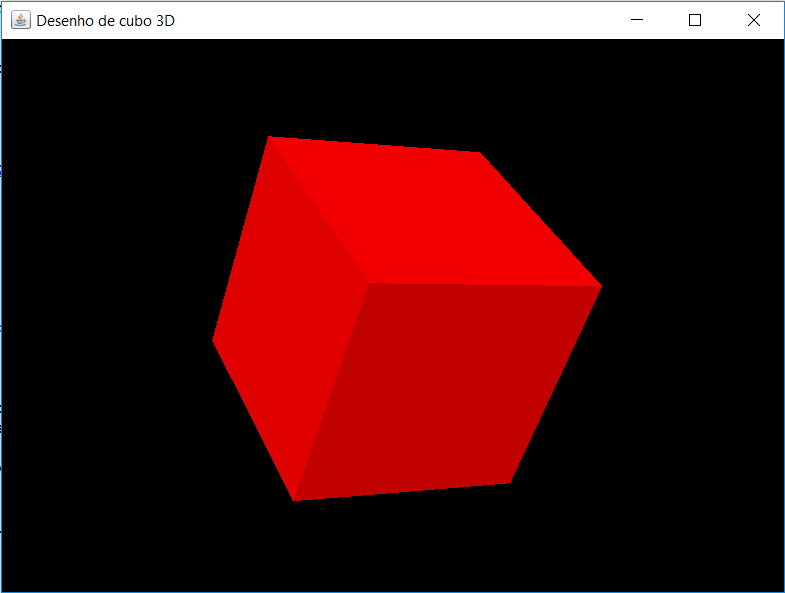
Faça o download do projeto clicando aqui.
Considerações finais
Esse artigo é a continuação do artigo sobre introdução a computação em 3D e, aqui, você estudou sobre como pintar uma forma geométrica representada em uma estrutura de vértices e arestas (veja o artigo de introdução). Você pôde entender a relação entre uma forma geométrica tridimensional pintada conforme fontes de iluminação e as cores de objetos do mundo real, em que, dadas as fontes de luz do ambiente, as faces do objeto assumem cores mais intensas ou mais escurecidas, conforme os ângulos de incidência de luz.
Então pessoal, chegamos ao final de mais um artigo sobre computação gráfica. Até a próxima!
