Introdução a computação em 3D
A computação gráfica, como o próprio nome já diz, se refere a computação de gráficos. Quando se pensa em computação gráfica, podem surgir questões como: Como é que os gráficos que representam uma imagem ou vídeo são computadas por um computador? Como formas em 3D de um jogo eletrônico são representadas e desenhadas na tela? Normalmente, um software de desenho permite o desenho de formas geométricas e, até, a criação de figuras mais complexas. Mas, que existem muitos softwares com essa finalidade muita gente já sabe. No entanto, como que esses softwares são feitos? Bom, todo software é criado através de uma, ou mais, linguagens de programação de alto ou baixo nível. Seja ele com finalidade de desenho, modelagem ou, até, um sistema operacional como o Microsoft Windows.
Então, como, através de uma linguagem de programação, desenhar formas em 3D? Por exemplo, um simples cubo? È necessário, primeiramente, entender a representação de dados referentes a geometria do objeto. Geralmente, essa estrutura é composta de vertices, arestas e faces. Cada aresta pode ter uma referência a cada um dos dois vértices que ela conecta, e, cada face, pode ter uma lista de referências de todos os vértices pertencentes a ela. Cada vértice, tem associado um vetor que são suas coordenadas relativas no universo virtual (ou ambiente onde a forma deve ser desenhada).
Após a explicação acima, você pode se perguntar: Por que é necessário representar assim as formas geométricas? A resposta é a seguinte, é necessário que os dados representantes da forma em 3D sejam compatíveis com operações de transformação geométrica. Essas operações de transformação devem ser aplicadas aos vértices da forma, de modo a atualzá-los com os valores referentes ao resultado da operação de transformação que pode ser, por exemplo, uma operação de rotação aplicada em um software que permite a visualização de objetos 3D em diversos ângulos.
No ambiente tridimensional, existem três eixos. No plano cartesiano de um ambiente 3D, esses eixos podem ser associados aos eixos do plano. Por exemplo, os eixos: X, Y e Z. Veja abaixo uma representação de um vértice no sistema de coordenadas cartesianas tridimensional:
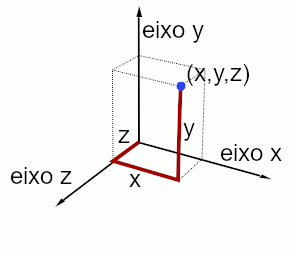
Vértices e arestas de um cubo
Agora, vejamos como calcular os vértices e arestas de um simples cubo. Lembrando que um cubo tem 8 vértices, 12 arestas e 6 faces. Para esse artigo, as faces não interessam, porque, por questões de simplificação, não será mostrado aqui, ainda, como distribuir cores nas faces de acordo com uma ou mais fontes de iluminação. Então, vamos calcular os vértices e arestas do cubo com base na medida do lado L do cubo e sua metade l. Veja abaixo:
l = L/2;
V1( -l, -l, -l );
V2( -l, l, -l );
V3( l, l, -l );
V4( l, -l, -l );
V5( -l, -l, l );
V6( -l, l, l );
V7( l, l, l );
V8( l, -l, l );
A1( V1, V2 );
A2( V2, V3 );
A3( V3, V4 );
A4( V4, V1 );
A5( V5, V6 );
A6( V6, V7 );
A7( V7, V8 );
A8( V8, V5 );
A9( V1, V5 );
A10( V2, V6 );
A11( V3, V7 );
A12( V4, V8 );
O código acima inicializa uma variável l com metade do lado do cubo. Logo em seguida, são calculadas as coordenadas (x, y, z) dos vértices com base na largura l. E, depois, são calculadas as arestas que conectam os vertices, formando os lados do cubo.
A rotação
Agora que já calculamos os vértices e arestas do cubo de modo que se possa desenhá-lo utilizando uma linguagem de programação, vamos entender como é possível rotacionar uma forma geométrica qualquer representada em uma estrutura de vértices e arestas.
Primeiramente, é necessário entender que a figura é representada por coordenadas referentes a três eixos de rotação. Com isso, é possível, por exemplo, determinar quais as coordenadas resultantes da rotação conforme um, ou mais, ângulos de rotação. Vale esclarecer que: As transformações geométricas, inclusive de rotação, são aplicadas sobre cada vértice do objeto 3D.
Como exemplo, podemos pensar o seguinte: Para rotacionar um objeto qualquer com os ângulos de rotação (X=30º, Y=15º e Z=135º) é necessário aplicar as rotações a todos os vértices do objeto. Ou seja, quais as coordenadas resultantes após a rotação de 30º em torno do eixo x, 15º em torno do eixo y e 135º em torno do eixo z?. Vale salientar que a ordem em que as rotações são aplicadas altera o resultado final. Se a rotação é aplicada em torno dos eixos na seguinte ordem: X, Y, Z, tem um resultado diferente do que na seguinte ordem: Y, X, Z.
Então vamos lá! Para entender a rotação em 3D, é necessário entender a rotação em 2D, pois, a rotação em 3D é uma extensão dela. Portanto, veja a seguir como realizar os cálculos para rotação em 2D.
Rotação em 2D
Para rotacionar uma forma qualquer, representada em 2D em uma estrutura de vértices e arestas, devemos calcular, para cada vértice da forma, as coordenadas dos vértices resultantes da operação de rotação. Veja a figura abaixo:
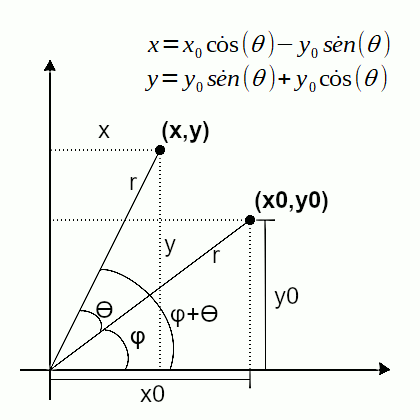
Queremos calcular o ponto (x,y) com base no ponto (x0,y0) e o angulo Ɵ. Repare nas fórmulas para se determinar o x e o y correspondentes ao resultado da rotação do vértice de coordenadas x0 e y0. Quando estiver estudando as fórmulas de rotação em 2D, volte a figura acima sempre que achar necessário. Então, veja abaixo o cálculo para se chegar a tais fórmulas:
Perceba na figura acima que:
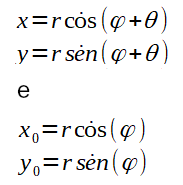
Assuma também a seguintes propriedades:
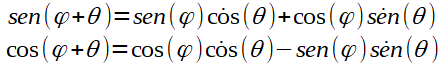
Substituindo:
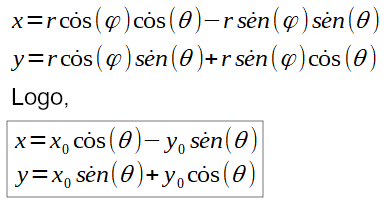
A seguir, veja como calcular o resultado da rotação em 3D com base nos cálculos de rotação em 2D vistos até aqui.
Rotação em 3D
Ao produzir um software que rotaciona formas geométricas em 3D, precisamos decidir sobre se a rotação segue a regra da mão esquerda ou regra da mão direita. Na física, é utilizada, geralmente, a regra da mão esquerda, por isso, vamos adotá-la aqui. Veja a figura abaixo que ilustra a regra da mão esquerda:
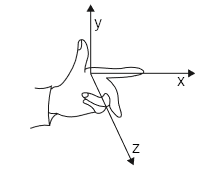
Perceba que, de acordo com a regra da mão esquerda, o polegar é posicionado na direção do eixo Y, o dedo indicador, na direção do eixo X e o dedo médio, na direção do eixo Z. Logo, a rotação em 2D pode ser aplicada para a rotação em 3D. Veja abaixo uma ilustração das direções de rotação utilizadas aqui:
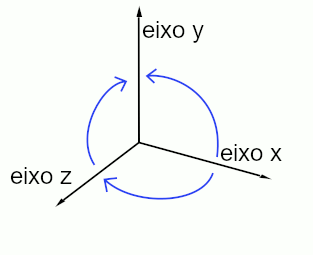
Então, veja como ficam as fórmulas de rotação em 3D:
Para a rotação em torno do eixo X, basta aplicar a fórmula de rotação em 2D, substituindo x e x0 por z e z0. Pois se quer rotacionar do z em direção ao y. Veja a figura e fórmulas abaixo:
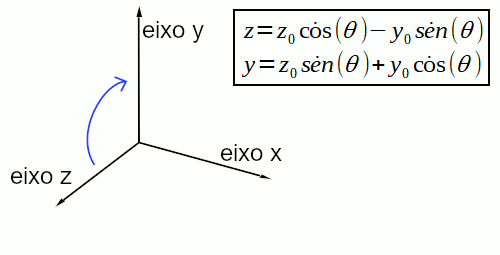
Já para rotação em torno do eixo Y, deve-se aplicar a fórmula, substituindo o valor de y e y0 por z e z0. Pois se deseja rotacionar do x em direção ao z. Veja a figura e fórmulas abaixo:
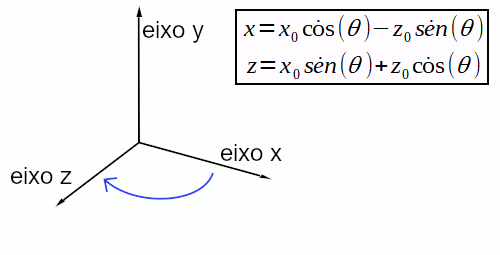
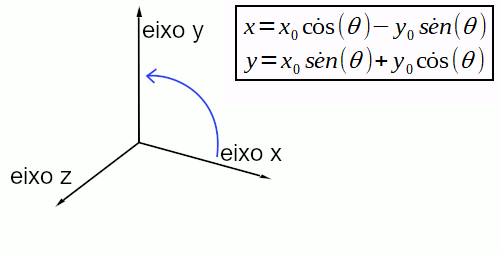
E para rotacionar em torno do eixo Z, é só aplicar a fórmula de rotação em 2D. Pois, se quer rotacionar do x em direção ao y. Veja a figura e fórmulas abaixo:
Atenção:
Esse método de cálculo de rotação é conhecido como Ângulos de Euler e, a maior parte dos autores
de trabalhos escritos sobre rotação e Ângulos de Euler, utiliza eixos organizados de modo diferente do apresentado aqui. Isso muda os
cálculos e fórmulas! Portanto, caso encontre algum outro material para estudar sobre o assunto, entenda que, talvez, esteja diferente do
ensinado aqui. Mas, isso não faz do conteúdo apresentado aqui, errado. Esse artigo, apenas, trata do problema resolvido com uma ordem
diferente dos eixos de rotação, com o eixo Y apontando para cima, o eixo X apontando para o lado direito e o eixo Z apontando na direção
da tela do computador. E é, também, utilizada aqui a regra da mão esquerda.
Então, após o esclarecimento acima, vejamos como fica o formato matricial, caso seja de sua preferência, para os cálculos dos vértices rotacionados segundo o método "Ângulos de Euler", aplicados na ordem Y, X, Z, com base nos ângulos (β, α, Ɣ):
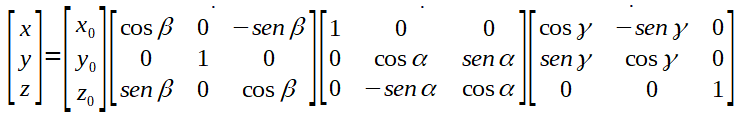
O resultado das multiplicações das matrizes gera as seguintes fórmulas:
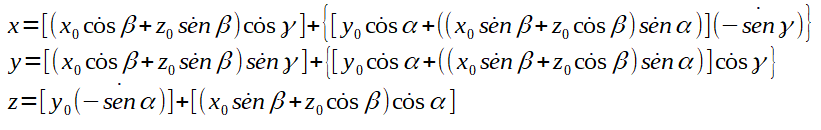
Translação e escala
Para transladar, basta adicionar o valor da translação pertinente a cada variável do vertice, e para escalar, basta multiplicar os fatores pelas variáveis do vertice. A translação e escala são muito mais simples de aplicar do que a rotação.
Observação:
Para diminuir o tamanho do objeto, basta aplicar uma escala com um valor menor que 1 e, para aumentar,
basta aplicar a escala com um valor maior que 1. Também é possível especificar escalas diferentes para diferentes coordenadas,
isto é, um escalar para X, um para Y e outro para Z!.
Veja as fórmulas abaixo:
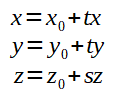
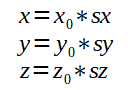
Projeção em perspectiva
Para projeção em perspectiva, é necessário aplicar a devida proporção a cada vértice da figura. A proporção é calculada em função da coordenada Z de cada vértice e uma distância focal que, na fórmula abaixo, é referenciada por D. veja a figura abaixo:
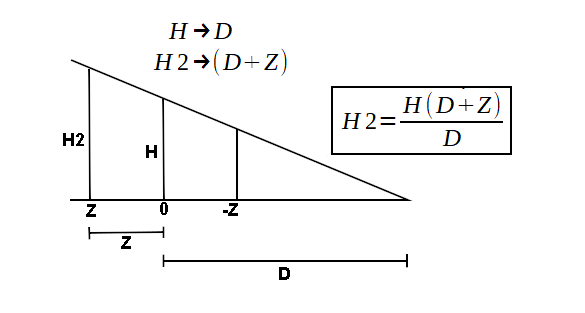
Ou seja, queremos encontrar o valor de H2 que é o novo valor da coordenada. Por exemplo, se quizermos calcular a proporção da projeção em perspectiva da coordenada X, é só substituir na fórmula acima o valor de H pelo valor de X e, o novo valor de X é o resultado do cálculo, ou seja, H2. A mesma lógica pode ser aplicada a coordenada Y.
Projeção na tela
Ao lidar com projeção em 3D, nos deparamos com um probleminha. Isto é, como projetar em 2D o que está representado em 3D? Isso porque nos temos as coordenadas (Vetores 3D) dos vértices da figura que queremos que seja desenhada. Mas, a tela do computador tem apenas duas dimensões. Para desenhar na tela do computador, podemos pintar pixels, linhas, polígonos em 2D, especificando coordenadas bidimensionais.
Perceba que, após a aplicação das transformações geométricas e/ou projeção em perspectiva sobre os vértices, se tem a projeção em 2D. Ou seja, já se pode descartar o valor da coordenada Z. Entenda que, a coordenada inicial, isto é, o ponto (x,y) = (0,0) é no canto inferior esquerdo da tela, o x da tela, cresce de traz para frente e o y da tela, cresce de cima para baixo. Mas, queremos projetar os vértices da figura relativos ao centro da tela e, queremos também, que o y cresça de baixo para cima, para plotarmos a figura como se estivessemos lidando com coordenadas no plano cartesiano, onde, o y cresce de baixo para cima, não de cima para baixo, e a coordenada (0,0) é no centro da tela. Então, para projetar em 2D, basta seguir a lógica abaixo:
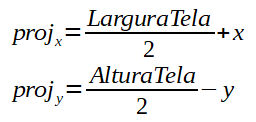
Perceba na figura acima que projx e projy são os valores resultantes da projeção. São coordenadas relativas ao centro da tela. Esta notação foi utilizada para diferenciar o valor do x e y dos resultados das projeções.
O programa
Desenvolvi um programa que desenha um cubo na tela e permite a rotação para visualização em diferentes ângulos. Foram implementados os dois métodos de rotação, isto é, o que foi apresentado primeiro e o que é resultado da multiplicação de matrizes que é equivalente ao primeiro. Você pode ver as implementações das rotações na classe Tranfomador! O código fonte está organizado em poucas classes, o que não é bom. Fiz assim apenas por questões didáticas. Porém, se o projeto tendesse a crescer, seria necessário organizá-lo de modo diferente: Em mais classes e interfaces.
Ao executar o programa, o modo de rotação começa configurado para rotação com base nos ângulos para os eixos X e Y. Caso deseje rotacionar em torno do eixo Z, basta pressionar a tecla "z" e arrastar e soltar com uso do mouse em direção ao eixo X. Para retornar ao modo de rotação com base nos ângulos X e Y, basta pressionar qualquer outra tecla diferente de "z" e arrastar e soltar com uso do mouse para rotacionar. Veja abaixo uma captura da janela do programa:
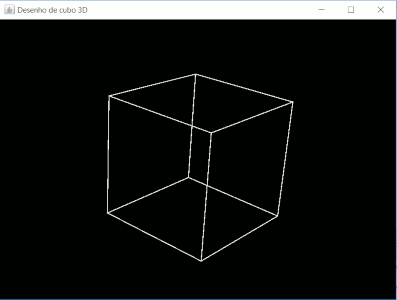
Faça o download do programa (com código fonte) como projeto netbeans clicando aqui.
Após fazer o download, experimente alterar o programa, estude-o! Recomendo que faça outra versão do seu jeito. Isto é, talvez você prefira mudar as direções dos eixos, alterar a ordem de rotação ou fazer alguma outra alteração, o que poderá implicar em realizar novos cálculos!
Considerações finais
Bom, chegamos ao final do artigo. Foi ensinado aqui sobre como representar os vértices e arestas de uma figura 3D, desenhar-la na tela do computador, rotacionar, transladar e escalar os vértices dela e calcular as coordenadas resultantes da projeção em perspectiva. No próximo artigo sobre computação gráfica, pretendo escrever sobre a representação e pintura das faces de um objeto 3D.
Veja um exemplo de aplicação dos conceitos aqui apresentados, e mais alguns conceitos não apresentados aqui, aplicados em um software/framework para plotagem de funções e objetos em 3D. Abaixo o link da página do projeto (experimente baixar e rodar o jar da biblioteca!):
Link da página do projeto Plot3D: clique aqui.
Até a próxima!
